

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Smarandache Number
المؤلف:
Sloane, N. J. A.
المصدر:
Sequences A007908, A058183, and A058935 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
19-11-2020
950
Consider the consecutive number sequences formed by the concatenation of the first 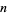 positive integers: 1, 12, 123, 1234, ... (OEIS A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). This sequence gives the digits of the Champernowne constant, and is sometimes also known as the Barbier infinite word (Allouche and Shallit 2003, pp. 114, 299, and 336). The terms up to
positive integers: 1, 12, 123, 1234, ... (OEIS A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). This sequence gives the digits of the Champernowne constant, and is sometimes also known as the Barbier infinite word (Allouche and Shallit 2003, pp. 114, 299, and 336). The terms up to 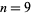 are given by
are given by
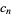 |
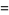 |
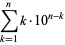 |
(1) |
 |
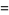 |
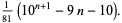 |
(2) |
These are sometimes called Smarandache consecutive numbers, but in this work, the terms in the sequence will be called simply Smarandache numbers. Similarly, a Smarandache number that is prime will be called a Smarandache prime. Surprisingly, no Smarandache primes 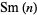 exist for
exist for 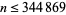 (Great Smarandache PRPrime search; Dec. 5, 2016).
(Great Smarandache PRPrime search; Dec. 5, 2016).
The number of digits of 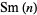 can be computed by noticing the pattern in the following table, where
can be computed by noticing the pattern in the following table, where
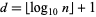 |
(3) |
is the number of digits in 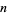 .
.
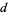 |
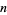 range range |
digits |
| 1 | 1-9 | 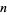 |
| 2 | 10-99 | 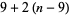 |
| 3 | 100-999 | 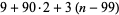 |
| 4 | 1000-9999 | 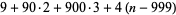 |
By induction, the number of digits 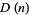 in
in 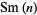 can be written
can be written
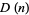 |
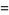 |
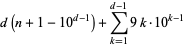 |
(4) |
 |
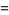 |
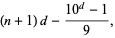 |
(5) |
where the second term is the repunit 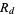 . For
. For 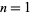 , 2, ..., the digit lengths
, 2, ..., the digit lengths 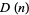 of
of 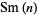 are therefore 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, ... (OEIS A058183).
are therefore 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, ... (OEIS A058183).

The results of concatenating the binary representations of the first few integers are 1, 110, 11011, 11011100, 11011100101, ... (OEIS A058935). These digit sequences are plotted above for 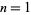 to 90. Interpreting the digit sequence as a binary fraction, the result is the binary Champernowne constant
to 90. Interpreting the digit sequence as a binary fraction, the result is the binary Champernowne constant 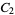 .
.
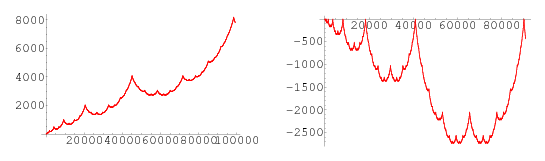
Interestingly, taking the cumulative sum 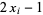 where
where {x_i}" src="https://mathworld.wolfram.com/images/equations/SmarandacheNumber/Inline34.gif" style="height:15px; width:21px" /> are the digits
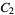 gives a plot showing batrachion-like structure (left figure), and doing the same with
gives a plot showing batrachion-like structure (left figure), and doing the same with {x_i}_(i=2)^infty" src="https://mathworld.wolfram.com/images/equations/SmarandacheNumber/Inline36.gif" style="height:17px; width:38px" /> (right figure) gives structures resembling the Blancmange function (and the Hofstadter-Conway $10,000 sequence).
REFERENCES:
--. "The Great Smarandache PRPrime search." https://smarandache.ddns.net:1200/server_stats.html.
Mudge, M. "Top of the Class." Personal Computer World, 674-675, June 1995.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Sloane, N. J. A. Sequences A007908, A058183, and A058935 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Stephan, R. W. "Factors and Primes in Two Smarandache Sequences." Smarandache Notions J. 9, 4-10, 1998.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.