A primefree sequence is sequence whose terms are never prime. Graham (1964) proved that there exist relatively prime positive integers 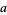 and 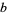 such that the recurrence equation

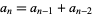(1)

with 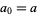 and 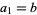 contains no prime numbers.

In addition, Graham (1964) constructed a pair of numbers (one 33 digits and the other 34)

			(2)
			(3)

satisfying this condition. Knuth (1990) subsequently found a 17-digit pair

			(4)
			(5)

satisfying the same conditions. Almost immediately, Wilf (1990) found a smaller pair (one 17 digits and the other 16)

			(6)
			(7)

Note that Hoffman (1998, p. 159) inadvertently inverted the order of the Wilf (1990) pair, thus obtaining a sequence that has prime terms for 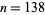, 163, 190, 523, 1855, 3228, 3579, 6468, 7170, 10230, 12783, 17259, 60139, 91315, 97923, 101823, 156075, 182220, ... (OEIS A108156), with no others for  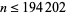(E. W. Weisstein, May 5, 2006).

Nicol (1999) subsequently found the 12-digit pair .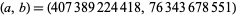

REFERENCES:

Graham, R. L. "A Fibonacci-Like Sequence of Composite Numbers." Math. Mag. 37, 322-324, 1964.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 11 and 252, 1994.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.

Knuth, D. E. "A Fibonacci-Like Sequence of Composite Numbers." Math. Mag. 63, 21-25, 1990.

Nicol, J. W. "A Fibonacci-Like Sequence of Composite Numbers." Elec. J. Combin. 6, R44, 1-6, 1999.

Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, p. 178, 1991.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 367, 1996.

Rivera, C. "Problem 31. Fibonacci-All Composites Sequence." https://www.primepuzzles.net/problems/prob_031.htm.

Sloane, N. J. A. Sequence A108156 in "The On-Line Encyclopedia of Integer Sequences."

Wilf, H. S. Letters to the Editor. Math. Mag. 63, 284, 1990.