

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Euclid,s Theorems
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M.
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
الجزء والصفحة:
...
12-9-2020
2962
A theorem sometimes called "Euclid's first theorem" or Euclid's principle states that if 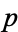 is a prime and
is a prime and 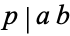 , then
, then 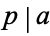 or
or 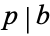 (where
(where 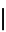 means divides). A corollary is that
means divides). A corollary is that 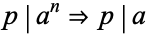 (Conway and Guy 1996). The fundamental theorem of arithmetic is another corollary (Hardy and Wright 1979).
(Conway and Guy 1996). The fundamental theorem of arithmetic is another corollary (Hardy and Wright 1979).
Euclid's second theorem states that the number of primes is infinite. This theorem, also called the infinitude of primes theorem, was proved by Euclid in Proposition IX.20 of the Elements (Tietze 1965, pp. 7-9). Ribenboim (1989) gives nine (and a half) proofs of this theorem. Euclid's elegant proof proceeds as follows. Given a finite sequence of consecutive primes 2, 3, 5, ..., 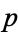 , the number
, the number
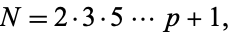 |
(1) |
known as the 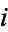 th Euclid number when
th Euclid number when 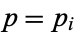 is the
is the 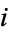 th prime, is either a new prime or the product of primes. If
th prime, is either a new prime or the product of primes. If  is a prime, then it must be greater than the previous primes, since one plus the product of primes must be greater than each prime composing the product. Now, if
is a prime, then it must be greater than the previous primes, since one plus the product of primes must be greater than each prime composing the product. Now, if 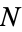 is a product of primes, then at least one of the primes must be greater than
is a product of primes, then at least one of the primes must be greater than 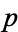 . This can be shown as follows.
. This can be shown as follows.
If 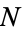 is composite and has no prime factors greater than
is composite and has no prime factors greater than 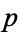 , then one of its factors (say
, then one of its factors (say 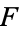 ) must be one of the primes in the sequence, 2, 3, 5, ...,
) must be one of the primes in the sequence, 2, 3, 5, ..., 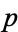 . It therefore divides the product
. It therefore divides the product 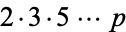 . However, since it is a factor of
. However, since it is a factor of 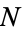 , it also divides
, it also divides 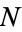 . But a number which divides two numbers
. But a number which divides two numbers 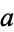 and
and 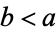 also divides their difference
also divides their difference 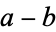 , so
, so 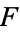 must also divide
must also divide
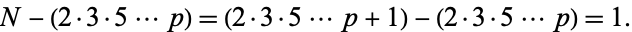 |
(2) |
However, in order to divide 1,  must be 1, which is contrary to the assumption that it is a prime in the sequence 2, 3, 5, .... It therefore follows that if
must be 1, which is contrary to the assumption that it is a prime in the sequence 2, 3, 5, .... It therefore follows that if  is composite, it has at least one factor greater than
is composite, it has at least one factor greater than 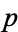 . Since
. Since 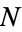 is either a prime greater than
is either a prime greater than 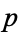 or contains a prime factor greater than
or contains a prime factor greater than 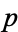 , a prime larger than the largest in the finite sequence can always be found, so there are an infinite number of primes. Hardy (1992) remarks that this proof is "as fresh and significant as when it was discovered" so that "two thousand years have not written a wrinkle" on it.
, a prime larger than the largest in the finite sequence can always be found, so there are an infinite number of primes. Hardy (1992) remarks that this proof is "as fresh and significant as when it was discovered" so that "two thousand years have not written a wrinkle" on it.
A similar argument shows that 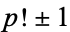 and
and
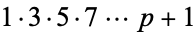 |
(3) |
must be either prime or be divisible by a prime 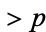 . Kummer used a variation of this proof, which is also a proof by contradiction. It assumes that there exist only a finite number of primes
. Kummer used a variation of this proof, which is also a proof by contradiction. It assumes that there exist only a finite number of primes 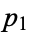 ,
, 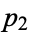 , ...,
, ..., 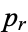 . Now define
. Now define 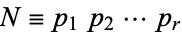 and consider
and consider 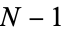 . It must be a product of primes, so it has a prime divisor
. It must be a product of primes, so it has a prime divisor 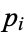 in common with
in common with 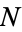 . Therefore,
. Therefore, 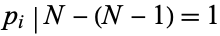 which is nonsense, so we have proved the initial assumption is wrong by contradiction.
which is nonsense, so we have proved the initial assumption is wrong by contradiction.
It is also true that there are runs of composite numbers which are arbitrarily long. This can be seen by defining
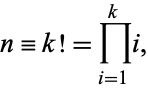 |
(4) |
where 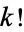 is a factorial. Then the
is a factorial. Then the 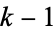 consecutive numbers
consecutive numbers 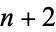 ,
, 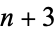 , ...,
, ..., 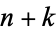 are composite, since
are composite, since
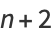 |
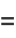 |
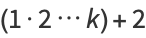 |
(5) |
 |
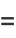 |
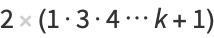 |
(6) |
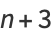 |
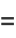 |
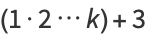 |
(7) |
 |
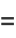 |
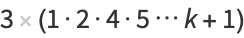 |
(8) |
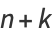 |
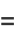 |
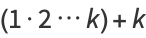 |
(9) |
 |
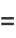 |
![k[1·2...(k-1)+1].](https://mathworld.wolfram.com/images/equations/EuclidsTheorems/Inline63.gif) |
(10) |
Guy (1981, 1988) points out that while  is not necessarily prime, letting
is not necessarily prime, letting 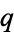 be the next prime after
be the next prime after  , the number
, the number 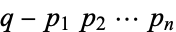 is conjectured always to be a prime known as a Fortunate prime, though this has not been proven.
is conjectured always to be a prime known as a Fortunate prime, though this has not been proven.
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 60, 1987.
Conway, J. H. and Guy, R. K. "There are Always New Primes!" In The Book of Numbers. New York: Springer-Verlag, pp. 133-134, 1996.
Cosgrave, J. B. "A Remark on Euclid's Proof of the Infinitude of Primes." Amer. Math. Monthly 96, 339-341, 1989.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 22, 1996.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, p. 34, 2004.
Dunham, W. "Great Theorem: The Infinitude of Primes." Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 73-75, 1990.
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 42-43, 2000.
Guy, R. K. §A12 in Unsolved Problems in Number Theory. New York: Springer-Verlag, 1981.
Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.
Hardy, G. H. A Mathematician's Apology. Cambridge, England: Cambridge University Press, 1992.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 28, 2003.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 3-12, 1989.
Tietze, H. Famous Problems of Mathematics: Solved and Unsolved Mathematics Problems from Antiquity to Modern Times. New York: Graylock Press, pp. 7-9, 1965.