In a 1847 talk to the Académie des Sciences in Paris, Gabriel Lamé (1795-1870) claimed to have proven Fermat's last theorem. However, Joseph Liouville immediately pointed out an error in Lamé's result by pointing out that Lamé had incorrectly assumed unique factorization in the ring of 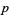-cyclotomic integers. Kummer had already studied the failure of unique factorization in cyclotomic fields and subsequently formulated a theory of ideals which was later further developed by Dedekind.

Kummer was able to prove Fermat's last theorem for all prime exponents falling into a class he called "regular." "Irregular" primes are thus primes that are not a member of this class, and a prime 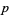 is irregular iff  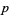divides the class number of the cyclotomic field generated by 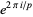. Equivalently, but more conveniently, an odd prime  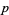is irregular iff  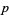divides the numerator of a Bernoulli number  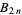with .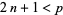

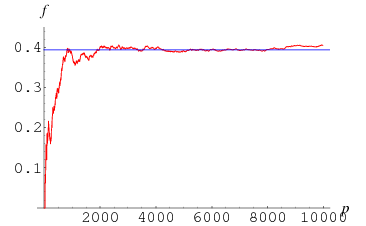
An infinite number of irregular primes exist, as proven in 1915 by Jensen (Vandiver and Wahlin 1928, p. 82; Carlitz 1954, 1968). In fact, Jensen also proved the slightly stronger result that there are an infinite number of irregular primes congruent to 5 (mod 6) (Carlitz 1968), a result subsequently improved by Montgomery (1965). The first few irregular primes are 37, 59, 67, 101, 103, 131, 149, 157, ... (OEIS A000928). Of the 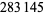 primes less than 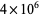,  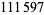(or 39.41%) are irregular. The conjectured fraction is  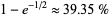(Ribenboim 1996, p. 415).

The numbers of irregular primes less than 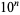 for 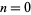, 1, 2, ... are 0, 0, 3, 64, 497, ... (OEIS A092901).

The largest known proven irregular prime as of Apr. 2009 is 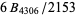, which has 10342 decimal digits and was found by M. Oakes et al. on Apr. 4, 2009 (https://primes.utm.edu/primes/page.php?id=87451). The largest known irregular probable prime is the numerator of 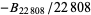, which has 71290 digits and was found by T. D. Noe on Sep. 28, 2005. The values of  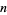such that  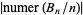is prime are 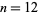, 16, 18, 26, 34, 36, 38, 42, 74, 114, 118, 396, 674, 1870, 4306, 22808, ... (OEIS A112548), with the corresponding values necessarily being irregular.

REFERENCES:

Buhler, J.; Crandall, R.; Ernvall, R.; and Metsänkylä, T. "Irregular Primes and Cyclotomic Invariants to Four Million." Math. Comput. 61, 151-153, 1993.

Buhler, J.; Crandall, R.; Ernvall, R.; Metsankyla, T.; and Shokrollahi, M. "Irregular Primes and Cyclotomic Invariants to 12 Million." J. Symb. Comput. 11, 1-8, 2000.

Buhler, J. P.; Crandall, R. E.; and Sompolski, R. W. "Irregular Primes to One Million." Math. Comput. 59, 717-722, 1992.

Caldwell, C. K. "The Prime Pages. The Top 20: irregular Primes." https://primes.utm.edu/top20/page.php?id=26.

Carlitz, L. "A Note on Irregular Primes." Proc. Amer. Math. Soc. 5, 329-331, 1954.

Carlitz, L. "Bernoulli Numbers." Fib. Quart. 6, 71-85, 1968.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 202, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 85, 2003.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 192, 1998.

Johnson, W. "Irregular Primes and Cyclotomic Invariants." Math. Comput. 29, 113-120, 1975.

Johnson, W. "Irregular Prime Divisors of the Bernoulli Numbers." Math. Comput. 28, 653-657, 1974.

Montgomery, H. L. "Distribution of Irregular Primes." Ill. J. Math. 9, 553-558, 1965.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 325-329 and 414-425, 1996.

Siegel, C. L. "Zu zwei Bemerkungen Kummers." Nachr. Akad. d. Wiss. Göttingen, Math. Phys. Kl. 2, 51-62, 1964.

Sloane, N. J. A. Sequences A000928/M5260, A092901, and A112548 in "The On-Line Encyclopedia of Integer Sequences."

Stewart, C. L. "A Note on the Fermat Equation." Mathematika 24, 130-132, 1977.

Vandiver, H. S. "On Developments in an Arithmetic Theory of the Bernoulli and Allied Numbers." Scripta Math. 25, 273-303, 1960.

Vandiver, H. S. and Wahlin, G. E. "Algebraic Numbers." Bull. Nat. Res. Council, No. 62, 1928.

Wagstaff, S. S.  Jr. "The Irregular Primes to 125000." Math. Comput. 32, 583-591, 1978.