The number 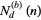 of digits  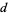in the base- 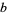representation of a number  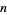is called the 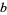-ary digit count for 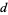. The digit count is implemented in the Wolfram Language as DigitCount[n, b, d].

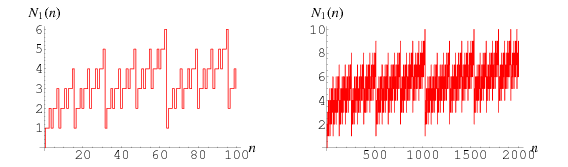
The number of 1s 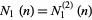 in the binary representation of a number 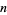, illustrated above, is given by

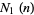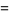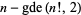			(1)
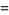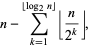			(2)

where 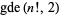 is the greatest dividing exponent of 2 with respect to 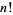. This is a special application of the general result that the power of a prime  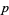dividing a factorial (Vardi 1991, Graham et al. 1994). Writing  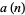for 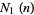, the number of 1s is also given by the recurrence relation

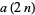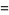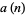			(3)
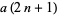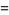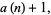			(4)

with 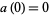, and by

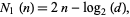(5)

where 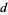 is the denominator of

(6)

For 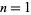, 2, ..., the first few values are 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, ... (OEIS A000120; Smith 1966, Graham 1970, McIlroy 1974).

For a binary number, the count of 1s 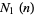 is equal to the digit sum 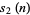. The quantity  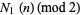is called the parity of a nonnegative integer .

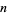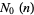 and 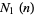 satisfy the beautiful identities

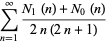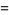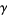			(7)
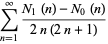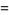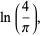			(8)

where 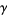 is the Euler-Mascheroni constant and  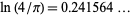(OEIS A094640) is its "alternating analog" (Sondow 2005).

Let 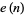 and 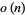 be the numbers of even and odd digits respectively of 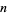. Then

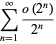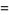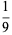			(9)
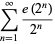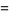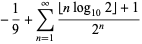			(10)
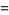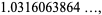			(11)

where the latter (OEIS A096614) is transcendental (Borwein et al. 2004, pp. 14-15).

REFERENCES:

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Graham, R. L. "On Primitive Graphs and Optimal Vertex Assignments." Ann. New York Acad. Sci. 175, 170-186, 1970.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Factorial Factors." §4.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 111-115, 1994.

McIlroy, M. D. "The Number of 1's in Binary Integers: Bounds and Extremal Properties." SIAM J. Comput. 3, 255-261, 1974.

Sloane, N. J. A. Sequences A000120/M0105, A094640, A096614 in "The On-Line Encyclopedia of Integer Sequences."

Smith, N. "Problem B-82." Fib. Quart. 4, 374-365, 1966.

Sondow, J. "New Vacca-type Rational Series for Euler's Constant and its 'alternating' Analog 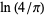." 1 Aug 2005. https://arxiv.org/abs/math.NT/0508042.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 33, 2004. https://www.mathematicaguidebooks.org/.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 67, 1991.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 902, 2002.