In 1913, Ramanujan asked if the Diophantine equation of second order

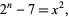sometimes called the Ramanujan-Nagell equation, has any solutions other than 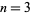, 4, 5, 7, and 15 (Schroeppel 1972, Item 31; Ramanujan 2000, p. 327; OEIS A060728). These correspond to 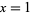, 3, 5, 11, and 181 (OEIS A038198). Nagell (1948) and Skolem et al. (1959) showed there are no solutions past 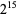, thus establishing Ramanujan's question in the negative.

A generalization to two variables  and 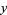 was considered by Euler (Engel 1998, p. 126).

REFERENCES:

Bundschuh, P. "On the Diophantine Equation of Ramanujan-Nagell." In Seminar on Diophantine Approximation. Papers from the Seminar Held in Yokohama, April 6-8, 1987. Yokohama, Japan: Keio University, Department of Mathematics, pp. 31-40, 1988.

Cohen, E. L. "On the Ramanujan-Nagell Equation and Its Generalizations." In Number Theory. Proceedings of the First Conference of the Canadian Number Theory Association held in Banff, Alberta, April 17-27, 1988 (Ed. R. A. Mollin). Berlin: de Gruyter, pp. 81-92, 1990.

Engel, A. Problem-Solving Strategies. New York: Springer-Verlag, 1998.

Johnson, W. "The Diophantine Equation 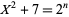." Amer. Math. Monthly 94. 59-62, 1987.

Mignotte, M. "Une nouvelle résolution de l'équation 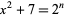." Rend. Sem. Fac. Sci. Univ. Cagliari 54, 41-43, 1984.

Mordell, L. J. Diophantine Equations. New York: Academic Press, p. 205, 1969.

Nagell, T. Nordisk Mat. Tidskr. 30, 62-64, 1948.

Nagell, T "The Diophantine Equation 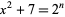." Arkiv för Mat. 4, 185-187, 1960.

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.

Ramasmay, A. M. S. "Ramanujan's Equation." J. Ramanujan Math. Soc. 7, 133-153, 1992.

Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., pp. 90-91, 1992.

Schroeppel, R. C. Item 31 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 14, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item31.

Skolem, T.; Chowla, S.; and Lewis, D. J. "The Diophantine Equation 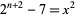 and Related Problems." Proc. Amer. Math. Soc. 10, 663-669, 1959.

Sloane, N. J. A. Sequences A038198 and A060728 in "The On-Line Encyclopedia of Integer Sequences."

Stewart, I. and Tall, D. Algebraic Number Theory. New York: Chapman and Hall, 1987.

Turnwald, G. "A Note on the Ramanujan-Nagell Equation, in Number-Theoretic Analysis." In Number-Theoretic Analysis. Proceedings of the Seminar Held at the University of Vienna and at the Technical University of Vienna, Vienna, 1988-1989 (Ed. H. Hlawka and R. F. Tichy). Berlin: Springer-Verlag, pp. 206-207, 1990.