

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Generalized Continued Fraction
المؤلف:
Borwein, J.; Bailey, D.; and Girgensohn, R.
المصدر:
Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
الجزء والصفحة:
...
2-5-2020
891
A generalized continued fraction is an expression of the form
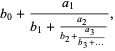 |
(1) |
where the partial numerators 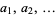 and partial denominators
and partial denominators 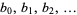 may in general be integers, real numbers, complex numbers, or functions (Rockett and Szüsz, 1992, p. 1). Generalized continued fractions may also be written in the forms
may in general be integers, real numbers, complex numbers, or functions (Rockett and Szüsz, 1992, p. 1). Generalized continued fractions may also be written in the forms
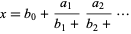 |
(2) |
or
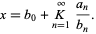 |
(3) |
Note that letters other than 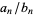 are sometimes also used; for example, the documentation for ContinuedFractionK[f, g,
are sometimes also used; for example, the documentation for ContinuedFractionK[f, g, {" src="https://mathworld.wolfram.com/images/equations/GeneralizedContinuedFraction/Inline4.gif" style="height:15px; width:5px" />i, imin, imax
}" src="https://mathworld.wolfram.com/images/equations/GeneralizedContinuedFraction/Inline5.gif" style="height:15px; width:5px" />] in the Wolfram Language uses
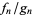 .
.
Padé approximants provide another method of expanding functions, namely as a ratio of two power series. The quotient-difference algorithm allows interconversion of continued fraction, power series, and rational function approximations.
A small sample of closed-form continued fraction constants is given in the following table (cf. Euler 1775). The Ramanujan continued fractions provide another fascinating class of continued fraction constants, and the Rogers-Ramanujan continued fraction is an example of a convergent generalized continued fraction function where a simple definition leads to quite intricate structure.
| continued fraction | value | approximate | OEIS |
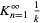 |
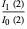 |
0.697774... | A052119 |
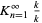 |
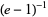 |
0.581976... | A073333 |
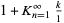 |
![sqrt(2/(epi))[erfc(2^(-1/2))]^(-1)](https://mathworld.wolfram.com/images/equations/GeneralizedContinuedFraction/Inline12.gif) |
1.525135... | A111129 |
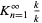 |
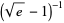 |
1.541494... | A113011 |
The value
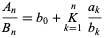 |
(4) |
is known as the 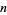 th convergent of the continued fraction.
th convergent of the continued fraction.
A regular continued fraction representation (which is usually what is meant when the term "continued fraction" is used without qualification) of a number  is one for which the partial quotients are all unity (
is one for which the partial quotients are all unity (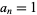 ),
), 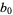 is an integer, and
is an integer, and 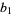 ,
, 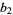 , ... are positive integers (Rockett and Szüsz, 1992, p. 3).
, ... are positive integers (Rockett and Szüsz, 1992, p. 3).
Euler showed that if a convergent series can be written in the form
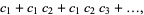 |
(5) |
then it is equal to the continued fraction
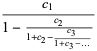 |
(6) |
(Borwein et al. 2004, p. 30).
To "round" a regular continued fraction, truncate the last term unless it is 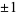 , in which case it should be added to the previous term (Gosper 1972, Item 101A). To take one over a simple continued fraction, add (or possibly delete) an initial 0 term. To negate, take the negative of all terms, optionally using the identity
, in which case it should be added to the previous term (Gosper 1972, Item 101A). To take one over a simple continued fraction, add (or possibly delete) an initial 0 term. To negate, take the negative of all terms, optionally using the identity
![[-a,-b,-c,-d,...]=[-a-1,1,b-1,c,d,...].](https://mathworld.wolfram.com/images/equations/GeneralizedContinuedFraction/NumberedEquation7.gif) |
(7) |
A particularly beautiful identity involving the terms of the continued fraction is
![([a_0,a_1,...,a_n])/([a_0,a_1,...,a_(n-1)])=([a_n,a_(n-1),...,a_1,a_0])/([a_n,a_(n-1),...,a_1]).](https://mathworld.wolfram.com/images/equations/GeneralizedContinuedFraction/NumberedEquation8.gif) |
(8) |
There are two possible representations for a finite simple fraction:
|
(9) |
REFERENCES:
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Gosper, R. W. "Continued fractions query." math-fun@cs.arizona.edu posting, Dec. 27, 1996.
Gosper, R. W. Item 101a in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, pp. 37-39, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/cf.html#item101a.
Rockett, A. M. and Szüsz, P. Continued Fractions. New York: World Scientific, 1992.