

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Modular Form
المؤلف:
Apostol, T. M
المصدر:
"Modular Forms with Multiplicative Coefficients." Ch. 6 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag
الجزء والصفحة:
...
24-12-2019
1848
Modular Form
A function 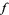 is said to be an entire modular form of weight
is said to be an entire modular form of weight 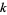 if it satisfies
if it satisfies
1. 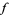 is analytic in the upper half-plane
is analytic in the upper half-plane 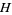 ,
,
2. 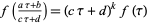 whenever
whenever ![[a b; c d]](http://mathworld.wolfram.com/images/equations/ModularForm/Inline6.gif) is a member of the modular group Gamma,
is a member of the modular group Gamma,
3. The Fourier series of 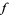 has the form
has the form
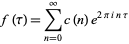 |
(1) |
Care must be taken when consulting the literature because some authors use the term "dimension 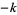 " or "degree
" or "degree 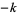 " instead of "weight
" instead of "weight 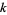 ," and others write
," and others write 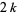 instead of
instead of 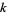 (Apostol 1997, pp. 114-115). More general types of modular forms (which are not "entire") can also be defined which allow poles in
(Apostol 1997, pp. 114-115). More general types of modular forms (which are not "entire") can also be defined which allow poles in 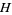 or at
or at 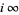 . Since Klein's absolute invariant
. Since Klein's absolute invariant 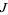 , which is a modular function, has a pole at
, which is a modular function, has a pole at 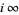 , it is a nonentire modular form of weight 0.
, it is a nonentire modular form of weight 0.
The set of all entire forms of weight 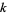 is denoted
is denoted 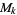 , which is a linear space over the complex field. The dimension of
, which is a linear space over the complex field. The dimension of 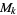 is 1 for
is 1 for 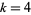 , 6, 8, 10, and 14 (Apostol 1997, p. 119).
, 6, 8, 10, and 14 (Apostol 1997, p. 119).
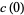 is the value of
is the value of 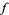 at
at 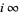 , and if
, and if 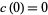 , the function is called a cusp form. The smallest
, the function is called a cusp form. The smallest 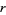 such that
such that 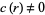 is called the order of the zero of
is called the order of the zero of 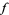 at
at 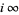 . An estimate for
. An estimate for 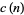 states that
states that
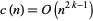 |
(2) |
if 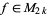 and is not a cusp form (Apostol 1997, p. 135).
and is not a cusp form (Apostol 1997, p. 135).
If 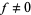 is an entire modular form of weight
is an entire modular form of weight 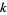 , let
, let 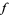 have
have 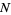 zeros in the closure of the fundamental region
zeros in the closure of the fundamental region 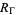 (omitting the vertices). Then
(omitting the vertices). Then
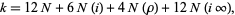 |
(3) |
where 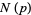 is the order of the zero at a point
is the order of the zero at a point 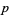 (Apostol 1997, p. 115). In addition,
(Apostol 1997, p. 115). In addition,
1. The only entire modular forms of weight 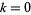 are the constant functions.
are the constant functions.
2. If 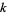 is odd,
is odd, 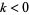 , or
, or 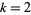 , then the only entire modular form of weight
, then the only entire modular form of weight 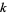 is the zero function.
is the zero function.
3. Every nonconstant entire modular form has weight 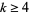 , where
, where 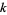 is even.
is even.
4. The only entire cusp form of weight 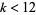 is the zero function.
is the zero function.
(Apostol 1997, p. 116).
For 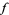 an entire modular form of even weight
an entire modular form of even weight 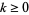 , define
, define 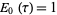 for all
for all  . Then
. Then 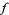 can be expressed in exactly one way as a sum
can be expressed in exactly one way as a sum
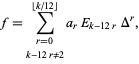 |
(4) |
where 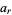 are complex numbers,
are complex numbers, 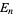 is an Eisenstein series, and
is an Eisenstein series, and 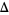 is the modular discriminant of the Weierstrass elliptic function. cusp forms of even weight
is the modular discriminant of the Weierstrass elliptic function. cusp forms of even weight 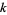 are then those sums for which
are then those sums for which 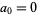 (Apostol 1997, pp. 117-118). Even more amazingly, every entire modular form
(Apostol 1997, pp. 117-118). Even more amazingly, every entire modular form 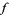 of weight
of weight 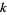 is a polynomial in
is a polynomial in 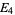 and
and 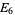 given by
given by
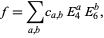 |
(5) |
where the 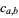 are complex numbers and the sum is extended over all integers
are complex numbers and the sum is extended over all integers 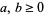 such that
such that 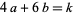 (Apostol 1998, p. 118).
(Apostol 1998, p. 118).
Modular forms satisfy rather spectacular and special properties resulting from their surprising array of internal symmetries. Hecke discovered an amazing connection between each modular form and a corresponding Dirichlet L-series. A remarkable connection between rational elliptic curves and modular forms is given by the Taniyama-Shimura conjecture, which states that any rational elliptic curve is a modular form in disguise. This result was the one proved by Andrew Wiles in his celebrated proof of Fermat's last theorem.
REFERENCES:
Apostol, T. M. "Modular Forms with Multiplicative Coefficients." Ch. 6 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 113-141, 1997.
Hecke, E. "Über Modulfunktionen und die Dirichlet Reihen mit Eulerscher Produktentwicklungen. I." Math. Ann. 114, 1-28, 1937.
Knopp, M. I. Modular Functions in Analytic Number Theory. New York: Chelsea, 1993.
Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.
Sarnack, P. Some Applications of Modular Forms. Cambridge, England: Cambridge University Press, 1993.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















