
Ternary
 المؤلف:
Erdős, P. and Graham, R. L.
المؤلف:
Erdős, P. and Graham, R. L.
 المصدر:
Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L,Enseignement Mathématique Université de Genève, Vol. 28
المصدر:
Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L,Enseignement Mathématique Université de Genève, Vol. 28
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-12-2019
14-12-2019
 2205
2205
Ternary
The base-3 method of counting in which only the digits 0, 1, and 2 are used. Ternary numbers arise in a number of problems in mathematics, including some problems of weighing. However, according to Knuth (1998), "no substantial application of balanced ternary notation has been made" (balanced ternary uses digits 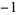 , 0, and 1 instead of 0, 1, and 2).
, 0, and 1 instead of 0, 1, and 2).

The illustration above shows a graphical representation of the numbers 0 to 25 in ternary, and the following table gives the ternary equivalents of the first few decimal numbers. The concatenation of the ternary digits of the consecutive numbers 0, 1, 2, 3, ... gives (0), (1), (2), (1, 0), (1, 1), (1, 2), (2, 0), ... (OEIS A054635).
| 1 |
1 |
11 |
102 |
21 |
210 |
| 2 |
2 |
12 |
110 |
22 |
211 |
| 3 |
10 |
13 |
111 |
23 |
212 |
| 4 |
11 |
14 |
112 |
24 |
220 |
| 5 |
12 |
15 |
120 |
25 |
221 |
| 6 |
20 |
16 |
121 |
26 |
222 |
| 7 |
21 |
17 |
122 |
27 |
1000 |
| 8 |
22 |
18 |
200 |
28 |
1001 |
| 9 |
100 |
19 |
201 |
29 |
1002 |
| 10 |
101 |
20 |
202 |
30 |
1010 |
Ternary digits have the following multiplication table.
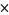 |
0 |
1 |
2 |
| 0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
| 2 |
0 |
2 |
11 |
A ternary representation can be used to uniquely identify totalistic cellular automaton rules, where the three colors (white, gray, and black) correspond to the three numbers 0, 1 and 2 (Wolfram 2002, pp. 60-70 and 886). For example, the ternary digits  , lead to the code 600 totalistic cellular automaton.
, lead to the code 600 totalistic cellular automaton.
Every even number represented in ternary has an even number (possibly 0) of 1s. This is true since a number is congruent mod 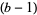 to the sum of its base-
to the sum of its base-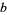 digits. In the case
digits. In the case 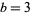 , there is only one digit (1) which is not a multiple of
, there is only one digit (1) which is not a multiple of 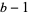 , so all we have to do is "cast out twos" and count the number of 1s in the base-3 representation.
, so all we have to do is "cast out twos" and count the number of 1s in the base-3 representation.
The following table gives 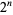 for
for 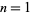 , 2, ... in ternary.
, 2, ... in ternary.
N. J. A. Sloane conjectured that for any integer 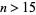 ,
, 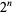 always has a 0 in its ternary expansion (Sloane 1973; Vardi 1991, p. 28). Known values of
always has a 0 in its ternary expansion (Sloane 1973; Vardi 1991, p. 28). Known values of 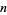 such that
such that 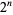 lacks a 0 are 1, 2, 3, 4, 15 (OEIS A102483), with no others up to
lacks a 0 are 1, 2, 3, 4, 15 (OEIS A102483), with no others up to 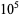 (E. W. Weisstein, Apr. 8, 2006). The positions (counting from the least significant ternary digits) of the first 0 digit in
(E. W. Weisstein, Apr. 8, 2006). The positions (counting from the least significant ternary digits) of the first 0 digit in 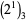 ,
, 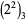 , ..., are 0, 0, 0, 0, 3, 2, 2, 4, 4, 5, 4, 2, 2, 4, 0, 3, 4, (OEIS A117971).
, ..., are 0, 0, 0, 0, 3, 2, 2, 4, 4, 5, 4, 2, 2, 4, 0, 3, 4, (OEIS A117971).
Similarly, 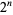 always has a 1 in its ternary expansion except for
always has a 1 in its ternary expansion except for 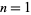 , 1, 3, and 9, with no others up to
, 1, 3, and 9, with no others up to 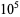 (E. W. Weisstein, Apr. 8, 2006).
(E. W. Weisstein, Apr. 8, 2006).
Erdős and Graham (1980) conjectured that no power of 2, 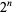 , for
, for 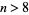 is a sum of distinct powers of 3. This is equivalent to the requirement that the ternary expansion of
is a sum of distinct powers of 3. This is equivalent to the requirement that the ternary expansion of 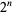 always contains a 2 for
always contains a 2 for 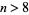 . The fact that the only values not having a two are
. The fact that the only values not having a two are 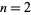 and 8 has been verified by Vardi (1991) up to
and 8 has been verified by Vardi (1991) up to 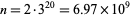 . The positions (counting from the least significant ternary digits) of the first 2 digit in
. The positions (counting from the least significant ternary digits) of the first 2 digit in 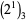 ,
, 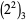 , ..., are 1, 0, 1, 2, 1, 4, 1, 0, 1, 2, 1, 3, 1, 3, ... (OEIS A117970).
, ..., are 1, 0, 1, 2, 1, 4, 1, 0, 1, 2, 1, 3, 1, 3, ... (OEIS A117970).
REFERENCES:
Erdős, P. and Graham, R. L. Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L'Enseignement Mathématique Université de Genève, Vol. 28, 1980.
Gardner, M. "The Ternary System." Ch. 11 in The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 104-112, 1984.
Knuth, D. E. The Art of Computer Programming. Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 173-175, 1998.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 10-11, 1991.
Sloane, N. J. A. Sequences A054635, A102483, A117970, and A117970 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. "The Persistence of a Number." J. Recr. Math. 6, 97-98, 1973.
Vardi, I. "The Digits of 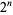 in Base Three." Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 20-25, 1991.
in Base Three." Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 20-25, 1991.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 60-70 and 886, 2002.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


