The base 2 method of counting in which only the digits 0 and 1 are used. In this base, the number 1011 equals 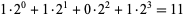. This base is used in computers, since all numbers can be simply represented as a string of electrically pulsed ons and offs. In computer parlance, one binary digit is called a bit, two digits are called a crumb, four digits are called a nibble, and eight digits are called a byte.

An integer 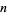 may be represented in binary in the Wolfram Language using the command BaseForm[n, 2], and the first  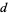digits of a real number  may be obtained in binary using RealDigits[x, 2, d]. Finally, a list of binary digits 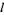 can be converted to a decimal rational number or integer using FromDigits[l, 2].

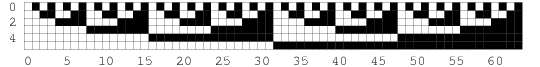
The illustration above shows the binary numbers from 0 to 63 represented graphically (Wolfram 2002, p. 117), and the following table gives the binary equivalents of the first few decimal numbers.

A negative number 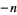 is most commonly represented in binary using the complement of the positive number 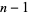, so 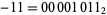 would be written as the complement of 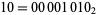, or 11110101. This allows addition to be carried out with the usual carrying and the leftmost digit discarded, so  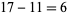gives

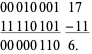The number of times 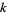 that a given binary number  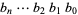is divisible by 2 is given by the position of the first  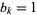counting from the right. For example,  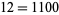is divisible by 2 twice, and  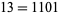is divisible by 2 zero times. The number of times that 1, 2, ... are divisible by 2 are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, 0, 1, 0, 2, ... (OEIS A007814), which is the binary carry sequence.

Real numbers can also be represented using binary notation by interpreting digits past the "decimal" point as negative powers of two, so the binary digits 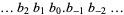 would represent the number

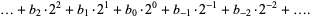Therefore, 1/2 would be represented as 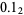, 1/4 as 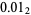, 3/4 as 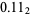, and so on. The sequence of binary digits for the integers 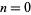, 1, ... concatenated together and interpreted as a binary constant give the binary Champernowne constant  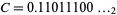(OEIS A030190).

Unfortunately, the storage of binary numbers in computers is not entirely standardized. Because computers store information in 8-bit bytes (where a bit is a single binary digit), depending on the "word size" of the machine, numbers requiring more than 8 bits must be stored in multiple bytes. The usual FORTRAN77 integer size is 4 bytes long. However, a number represented as (byte1 byte2 byte3 byte4) in a VAX would be read and interpreted as (byte4 byte3 byte2 byte1) on a Sun. The situation is even worse for floating-point (real) numbers, which are represented in binary as a mantissa and characteristic, and worse still for long (8-byte) reals!

Binary multiplication of single bit numbers (0 or 1) is equivalent to the AND operation, as can be seen in the following multiplication table.

	0	1
0	0	0
1	0	1

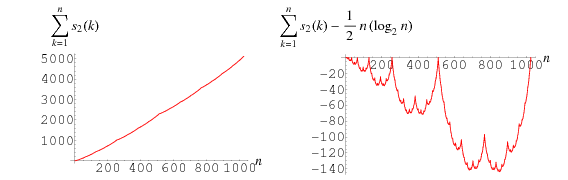
Consider the cumulative digit sum of all binary numbers up to 1, 2, ..., 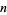. The first few terms are then 1, 2, 4, 5, 7, 9, 12, 13, 15, 17, 20, 22, ... (OEIS A000788). This sequence in monotonic increasing (left figure), but if the main asymptotic term is removed, a sequence of humped curves (right figure; Trott 2004, p. 218) tending towards the Blancmange function is obtained.

REFERENCES:

Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Factorial Factors." §4.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 111-115, 1994.

Heath, F. G. "Origin of the Binary Code." Sci. Amer. 227, 76-83, Aug. 1972.

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 6-9, 1991.

Pappas, T. "Computers, Counting, & Electricity." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 24-25, 1989.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Error, Accuracy, and Stability" and "Diagnosing Machine Parameters." §1.2 and §20.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 18-21, 276, and 881-886, 1992.

Sloane, N. J. A. Sequences A000788/M0964, A007814, and A030190 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 42-44, 1986.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 117, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمع العلمي للقرآن الكريم يصدر الكتاب الثاني من سلسلة يخشى

قسم الشعائر يكرّم أصحاب المواكب المشاركة في إحياء ذكرى شهادة السيدة الزهراء (عليها السلام)

جامعة العميد تستقبل طلبة المراحل الأولى المقبولين ضمن كلياتها للعام الدراسي الجديد

سماحة السيد الصافي يكرّم طلبة حفظ القرآن الكريم المتفوّقين ويؤكّد دور التدبّر في الهداية والتكامل

المزيد

الآخبار الصحية

طبيب يكشف تأثير برودة الشتاء على النوم

دون أن تعلم.. 10 عادات يومية تسرع شيخوخة جسمك

تقرير: النيكوتين خطر على القلب مهما كانت الطريقة

أيهما أفضل لصحتك.. زبدة الفول السوداني أم النوتيلا؟

المزيد

الآخبار التكنلوجية

السعودية تدشن أكبر نظام لتخزين الكهرباء بالبطاريات في العالم !

بأمر تنفيذي.. ترامب يؤكد هدف عودة الأميركيين إلى القمر في عام 2028

بعيدا عن البشر.. "قتال جوي في الفضاء" بين أميركا والصين

كشف مذهل في قاع "برمودا" !

المزيد