

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Pisot Number
المؤلف:
Bertin, M. J. and Pathiaux-Delefosse, A
المصدر:
Conjecture de Lehmer et petits nombres de Salem. Kingston: Queen,s Papers in Pure and Applied Mathematics, 1989.
الجزء والصفحة:
...
18-10-2019
1265
Pisot Number
A Pisot number is a positive algebraic integer greater than 1 all of whose conjugate elements have absolute value less than 1. A real quadratic algebraic integer greater than 1 and of degree 2 or 3 is a Pisot number if its norm is equal to 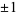 . The golden ratio
. The golden ratio 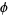 (denoted
(denoted 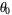 when considered as a Pisot number) is an example of a Pisot number since it has degree two and norm
when considered as a Pisot number) is an example of a Pisot number since it has degree two and norm 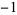 .
.
The smallest Pisot number is given by the positive root 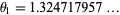 (OEIS A060006) of
(OEIS A060006) of
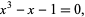 |
(1) |
known as the plastic constant. This number was identified as the smallest known by Salem (1944), and proved to be the smallest possible by Siegel (1944).
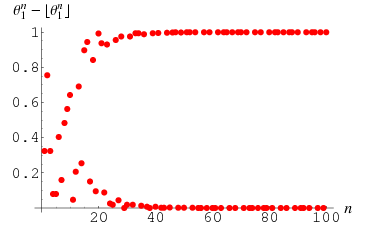
Pisot constants give rise to almost integers. For example, the larger the power to which 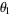 is taken, the closer
is taken, the closer 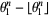 , where
, where 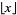 is the floor function, is to either 0 or 1 (Trott 2004). For example, the spectacular example
is the floor function, is to either 0 or 1 (Trott 2004). For example, the spectacular example 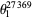 is within
is within 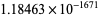 of an integer (Trott 2004, pp. 8-9).
of an integer (Trott 2004, pp. 8-9).
The powers of 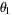 for which this quantity is closer to 0 are 1, 3, 4, 5, 6, 7, 8, 11, 12, 14, 17, ... (OEIS A051016), while those for which it is closer to 1 are 2, 9, 10, 13, 15, 16, 18, 20, 21, 23, ... (OEIS A051017).
for which this quantity is closer to 0 are 1, 3, 4, 5, 6, 7, 8, 11, 12, 14, 17, ... (OEIS A051016), while those for which it is closer to 1 are 2, 9, 10, 13, 15, 16, 18, 20, 21, 23, ... (OEIS A051017).
Siegel also identified the second smallest Pisot numbers as the positive root 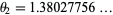 (OEIS A086106) of
(OEIS A086106) of
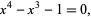 |
(2) |
showed that 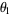 and
and 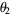 are isolated, and showed that the positive roots of each polynomial
are isolated, and showed that the positive roots of each polynomial
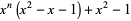 |
(3) |
for 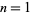 , 2, 3, ...,
, 2, 3, ...,
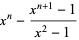 |
(4) |
for 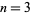 , 5, 7, ..., and
, 5, 7, ..., and
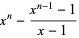 |
(5) |
for 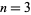 , 5, 7, ... are Pisot numbers.
, 5, 7, ... are Pisot numbers.
All the Pisot numbers less than 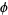 are known (Dufresnoy and Pisot 1955). Some small Pisot numbers and their polynomials are given in the following table. The latter two entries are from Boyd (1977).
are known (Dufresnoy and Pisot 1955). Some small Pisot numbers and their polynomials are given in the following table. The latter two entries are from Boyd (1977).
| number | Sloane | order | polynomial coefficients |
| 1.3247179572 | A060006 | 3 | 1 0 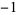 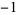 |
| 1.3802775691 | A086106 | 4 | 1 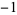 0 0 0 0 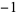 |
| 1.6216584885 | 16 | 1 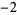 2 2 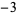 2 2 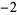 1 0 0 1 1 0 0 1 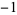 2 2 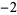 2 2 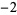 1 1 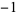 |
|
| 1.8374664495 | 20 | 1 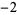 0 1 0 1 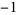 0 1 0 1 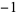 0 1 0 0 1 0 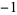 0 1 0 1 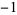 0 1 0 1 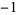 0 1 0 1 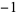 |
Pisot numbers originally arose in the consideration of
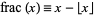 |
(6) |
where 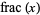 denotes the fractional part of
denotes the fractional part of  and
and 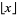 is the floor function. Letting
is the floor function. Letting 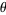 be a number greater than 1 and
be a number greater than 1 and 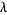 a positive number, for a given
a positive number, for a given 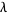 , the sequence of numbers
, the sequence of numbers 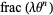 for
for 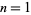 , 2, ... is an equidistributed sequence in the interval (0, 1) when
, 2, ... is an equidistributed sequence in the interval (0, 1) when 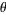 does not belong to a
does not belong to a 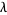 -dependent exceptional set
-dependent exceptional set 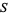 of measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional values of
of measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional values of 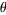 , and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers.
, and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers.
Pisot (1938) subsequently proved the fact that if 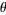 is chosen such that there exists a
is chosen such that there exists a 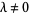 for which the series
for which the series
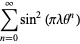 |
(7) |
converges, then 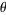 is an algebraic integer whose conjugates all (except for itself) have modulus
is an algebraic integer whose conjugates all (except for itself) have modulus 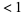 , and
, and 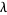 is an algebraic integer of the field
is an algebraic integer of the field 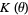 . Vijayaraghavan (1940) proved that the set of Pisot numbers has infinitely many limit points. Salem (1944) proved that the set of Pisot numbers is closed. The proof of this theorem is based on the lemma that for a Pisot number
. Vijayaraghavan (1940) proved that the set of Pisot numbers has infinitely many limit points. Salem (1944) proved that the set of Pisot numbers is closed. The proof of this theorem is based on the lemma that for a Pisot number 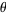 , there always exists a number
, there always exists a number 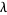 such that
such that 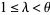 and the following inequality is satisfied:
and the following inequality is satisfied:
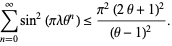 |
(8) |
REFERENCES:
Bell, J. P. and Hare, K. G. "Properties of 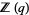 for
for 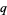 a Pisot number." http://www.math.uwaterloo.ca/~kghare/Preprints/PDF/P17_Zq.pdf.
a Pisot number." http://www.math.uwaterloo.ca/~kghare/Preprints/PDF/P17_Zq.pdf.
Bertin, M. J. and Pathiaux-Delefosse, A. Conjecture de Lehmer et petits nombres de Salem. Kingston: Queen's Papers in Pure and Applied Mathematics, 1989.
Bertin, M. J.; Decomps-Guilloux, A.; Grandet-Hugot, M.; Pathiaux-Delefosse, M.; and Schreiber, J. P. Pisot and Salem Numbers. Basel: Birkhäuser, 1992.
Borwein, P. and Hare, K. G. "Some Computations on Pisot and Salem Numbers." CECM-00:148, 18 May. http://www.cecm.sfu.ca/preprints/2000pp.html#00:148.
Boyd, D. W. "Small Salem Numbers." Duke Math. J. 44, 315-328, 1977.
Boyd, D. W. "Pisot and Salem Numbers in Intervals of the Real Line." Math. Comput. 32, 1244-1260, 1978.
Boyd, D. W. "Pisot Numbers in the Neighbourhood of a Limit Point. II." Math. Comput. 43, 593-602, 1984.
Boyd, D. W. "Pisot Numbers in the Neighbourhood of a Limit Point. I." J. Number Theory 21, 17-43, 1985.
Dubickas, A. "A Note on Powers of Pisot Numbers." Publ. Math. Debrecen 56, 141-144, 2000.
Dufresnoy, J. and Pisot, C. "Étude de certaines fonctions méromorphes bornées sur le cercle unité, application à un ensemble fermé d'entiers algébriques." Ann. Sci. École Norm. Sup. 72, 69-92, 1955.
Erdős, P.; Joó, M.; and Schnitzer, F. J. "On Pisot Numbers." Ann. Univ. Sci. Budapest, Eőtvős Sect. Math. 39, 95-99, 1997.
Katai, I. and Kovacs, B. "Multiplicative Functions with Nearly Integer Values." Acta Sci. Math. 48, 221-225, 1985.
Koksma, J. F. "Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins." Comp. Math. 2, 250-258, 1935.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 38 and 148, 1983.
Luca, F. "On a Question of G. Kuba." Arch. Math. (Basel) 74, 269-275, 2000.
Pisot, C. "La répartition modulo 1 et les nombres algébriques." Annali di Pisa 7, 205-248, 1938.
Salem, R. "Sets of Uniqueness and Sets of Multiplicity." Trans. Amer. Math. Soc. 54, 218-228, 1943.
Salem, R. "A Remarkable Class of Algebraic Numbers. Proof of a Conjecture of Vijayaraghavan." Duke Math. J. 11, 103-108, 1944.
Salem, R. "Power Series with Integral Coefficients." Duke Math. J. 12, 153-172, 1945.
Siegel, C. L. "Algebraic Numbers whose Conjugates Lie in the Unit Circle." Duke Math. J. 11, 597-602, 1944.
Sloane, N. J. A. Sequences A051016, A051017, A060006, and A086106 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Vijayaraghavan, T. "On the Fractional Parts of the Powers of a Number, II." Proc. Cambridge Phil. Soc. 37, 349-357, 1941.















 قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر كتاب (سر الرضا) ضمن سلسلة (نمط الحياة)
قسم الشؤون الفكرية يصدر كتاب (سر الرضا) ضمن سلسلة (نمط الحياة)

















