The Jacobi triple product is the beautiful identity

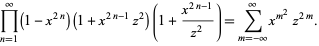(1)

In terms of the Q-functions, (1) is written

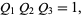(2)

which is one of the two Jacobi identities. In q-series notation, the Jacobi triple product identity is written

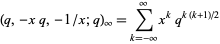(3)

for 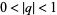 and 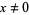 (Gasper and Rahman 1990, p. 12; Leininger and Milne 1999). Another form of the identity is

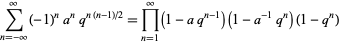(4)

(Hirschhorn 1999).

Dividing (4) by 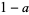 and letting  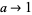gives the limiting case

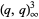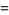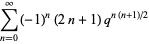			(5)
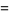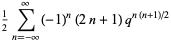			(6)

(Jacobi 1829; Hardy and Wright 1979; Hardy 1999, p. 87; Hirschhorn 1999; Leininger and Milne 1999).

For the special case of 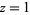, (◇) becomes

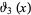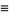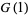			(7)
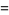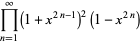			(8)
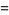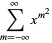			(9)
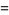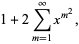			(10)

where 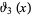 is a Jacobi elliptic function. In terms of the two-variable Ramanujan theta function 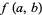, the Jacobi triple product is equivalent to

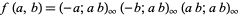(11)

(Berndt et al. 2000).

One method of proof for the Jacobi identity proceeds by defining the function

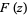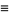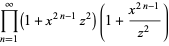			(12)
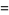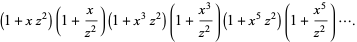			(13)

Then

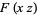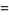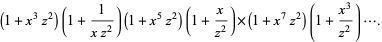(14)

Taking (14) 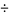 (13),

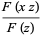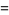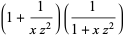			(15)
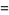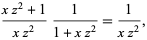			(16)

which yields the fundamental relation

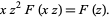(17)

Now define

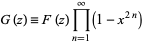(18)

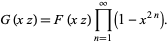(19)

Using (17), (19) becomes

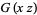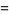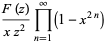			(20)
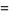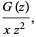			(21)

so

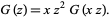(22)

Expand 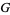 in a Laurent series. Since  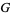is an even function, the Laurent series contains only even terms.

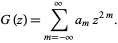(23)

Equation (22) then requires that

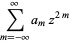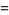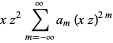			(24)
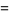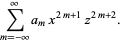			(25)

This can be re-indexed with 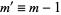 on the left side of (25)

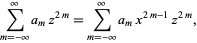(26)

which provides a recurrence relation

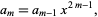(27)

so

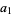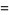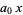			(28)
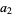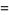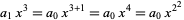			(29)
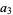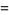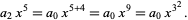			(30)

The exponent grows greater by 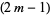 for each increase in  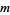of 1. It is given by

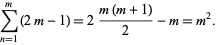(31)

Therefore,

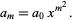(32)

This means that

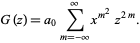(33)

The coefficient 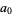 must be determined by going back to (◇) and (◇) and letting 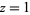. Then

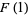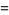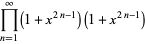			(34)
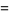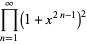			(35)
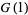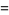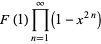			(36)
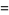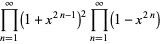			(37)
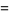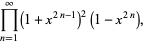			(38)

since multiplication is associative. It is clear from this expression that the 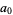 term must be 1, because all other terms will contain higher powers of . Therefore,

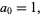(39)

so we have the Jacobi triple product,

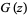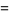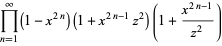			(40)
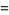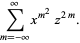			(41)

REFERENCES:

Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 222, 2007.

Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.

Borwein, J. M. and Borwein, P. B. "Jacobi's Triple Product and Some Number Theoretic Applications." Ch. 3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 62-101, 1987.

Foata, D. and Han, G.-N. "The Triple, Quintuple and Septuple Product Identities Revisited." In The Andrews Festschrift (Maratea, 1998): Papers from the Seminar in Honor of George Andrews on the Occasion of His 60th Birthday Held in Maratea, August 31-September 6, 1998. Sém. Lothar. Combin. 42, Art. B42o, 1-12, 1999 (electronic).

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.

Jacobi, C. G. J. Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, p. 90, 1829.

Leininger, V. E. and Milne, S. C. "Expansions for 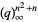 and Basic Hypergeometric Series in 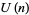." Discr. Math. 204, 281-317, 1999.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, p. 470, 1990.