

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Rogers-Ramanujan Continued Fraction
المؤلف:
Andrews, G.
المصدر:
On the General Rogers-Ramanujan Theorem. Providence, RI: Amer. Math. Soc., 1974.
الجزء والصفحة:
...
1-9-2019
3793
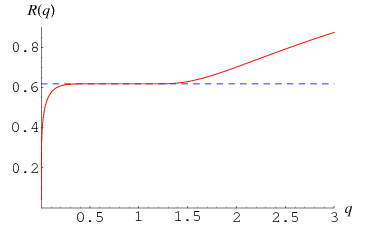
The Rogers-Ramanujan continued fraction is a generalized continued fraction defined by
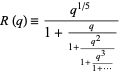 |
(1) |
(Rogers 1894, Ramanujan 1957, Berndt et al. 1996, 1999, 2000). It was discovered by Rogers (1894), independently by Ramanujan around 1913, and again independently by Schur in 1917. Modulo the factor of 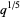 added for convenience, it provides a geometric series q-analog of the golden ratio
added for convenience, it provides a geometric series q-analog of the golden ratio
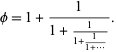 |
(2) |
The convergents 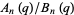 of
of 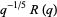 are given by
are given by
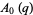 |
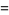 |
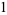 |
(3) |
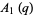 |
 |
 |
(4) |
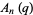 |
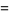 |
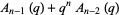 |
(5) |
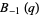 |
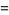 |
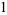 |
(6) |
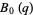 |
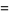 |
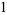 |
(7) |
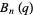 |
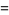 |
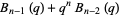 |
(8) |
(OEIS A128915 and A127836; Sills 2003, p. 25, identity 3-14).
The fraction can be expressed in closed form in terms of q-series by
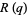 |
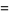 |
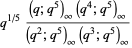 |
(9) |
 |
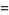 |
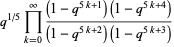 |
(10) |
 |
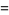 |
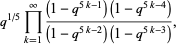 |
(11) |
and in terms of the Ramanujan theta function
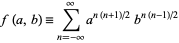 |
(12) |
by
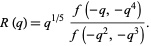 |
(13) |
In the upper half-plane and modulo branch cuts, it can also be expressed exactly in terms of the Dedekind eta function 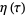 by
by
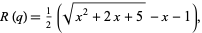 |
(14) |
where
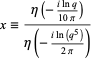 |
(15) |
(Trott 2004).
The coefficients of 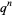 in the Maclaurin series of
in the Maclaurin series of 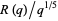 for
for 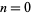 , 1, 2, ... are 1,
, 1, 2, ... are 1, 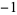 , 1, 0,
, 1, 0, 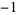 , 1,
, 1, 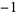 , 1, 0,
, 1, 0, 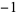 , 2,
, 2, 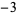 , ... (OEIS A007325).
, ... (OEIS A007325).
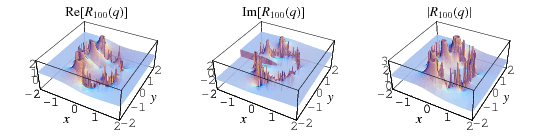
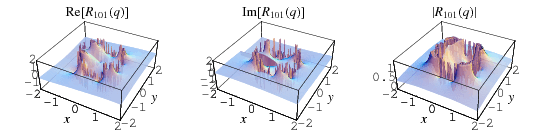
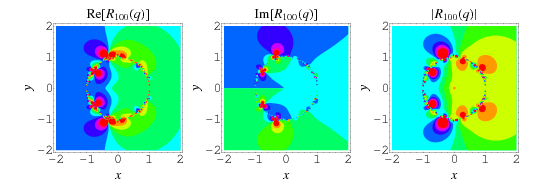
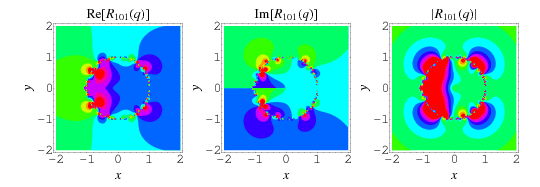
The fraction converges quickly for points sufficiently far from the unit circle in the complex plane. For values 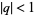 , the series converges to a unique value, while for
, the series converges to a unique value, while for 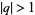 , it converges to two possible values. The value of the
, it converges to two possible values. The value of the 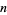 th convergent of the continued fraction
th convergent of the continued fraction 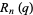 can be expressed in terms of the unique value inside the unit disk as
can be expressed in terms of the unique value inside the unit disk as
|
(16) |
(Andrews et al. 1992, Trott 2004).
Amazingly, Ramanujan showed that 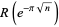 is an algebraic number for all positive rational
is an algebraic number for all positive rational 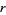 . Special cases include
. Special cases include
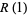 |
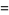 |
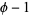 |
(17) |
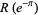 |
 |
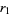 |
(18) |
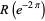 |
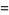 |
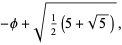 |
(19) |
where 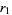 is the root of
is the root of 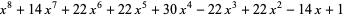 near 0.51142....
near 0.51142.... 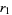 can be written as
can be written as
![r_1=1/8(3+sqrt(5))(RadicalBox[5, 4]-1)(sqrt(10+2sqrt(5))-(3+RadicalBox[5, 4])(RadicalBox[5, 4]-1))](http://mathworld.wolfram.com/images/equations/Rogers-RamanujanContinuedFraction/NumberedEquation8.gif) |
(20) |
(Yi 2001, Trott 2004). The values of 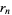 have been computed by Trott for all values of
have been computed by Trott for all values of 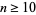 , and the algebraic degrees of
, and the algebraic degrees of 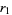 ,
, 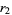 , ... are 8, 4, 32, 8, 40, 16, 64, 16, 96, 20, ... (OEIS A082682; Trott 2004).
, ... are 8, 4, 32, 8, 40, 16, 64, 16, 96, 20, ... (OEIS A082682; Trott 2004).
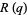 satisfies the amazing equalities
satisfies the amazing equalities
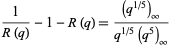 |
(21) |
![1/([R(q)]^5)-11-[R(q)]^5=((q)_infty^6)/(q(q^5)_infty^6),](http://mathworld.wolfram.com/images/equations/Rogers-RamanujanContinuedFraction/Inline64.gif) |
(22) |
where 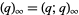 is a q-Pochhammer symbol. It also satisfies
is a q-Pochhammer symbol. It also satisfies
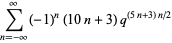 |
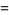 |
![[3/([R(q)]^2)+[R(q)]^3]q^(2/5)(q^5)_infty^3](http://mathworld.wolfram.com/images/equations/Rogers-RamanujanContinuedFraction/Inline68.gif) |
(23) |
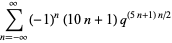 |
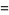 |
![[1/([R(q)]^3)-3[R(q)]^2]q^(3/5)(q^5)_infty^3](http://mathworld.wolfram.com/images/equations/Rogers-RamanujanContinuedFraction/Inline71.gif) |
(24) |
(Watson 1929ab; Berndt 1991, pp. 265-267; Berndt et al. 1996, 2000; Son 1998).
Defining
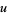 |
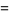 |
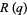 |
(25) |
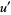 |
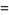 |
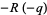 |
(26) |
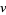 |
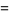 |
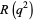 |
(27) |
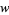 |
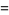 |
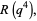 |
(28) |
these quantities satisfy the modular equations
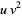 |
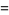 |
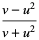 |
(29) |
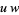 |
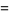 |
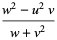 |
(30) |
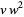 |
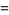 |
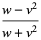 |
(31) |
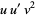 |
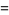 |
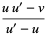 |
(32) |
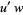 |
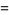 |
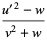 |
(33) |
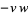 |
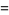 |
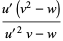 |
(34) |
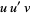 |
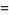 |
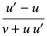 |
(35) |
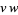 |
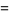 |
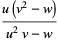 |
(36) |
(Berndt et al. 1996, 2000). Trott (2004) gives modular equations of orders 2 to 15 and the primes 17, 19, and 23.
As discussed by Hardy (Ramanujan 1962, pp. xxvii and xxviii), Berndt and Rankin (1995), and Berndt et al. (1996, 2000), Ramanujan also defined the generalized continued fraction
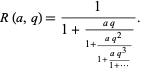 |
(37) |
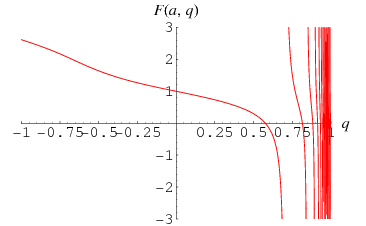

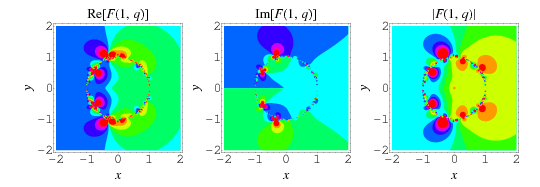
Ramanujan also considered the continued fraction
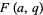 |
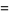 |
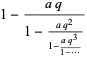 |
(38) |
 |
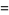 |
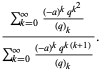 |
(39) |
(Berndt 1991, p. 30; Berndt et al. 1996, 2000), of which the special case 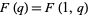 is plotted above.
is plotted above.
Terminating at a term 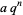 gives
gives
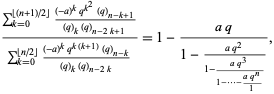 |
(40) |
(Berndt et al. 1996, 2000).
The real roots of 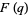 are 0.576149, 0.815600, 0.882493, 0.913806, 0.931949, 0.943785, 0.952125, ..., the smallest of which was found by Ramanujan (Berndt et al. ).
are 0.576149, 0.815600, 0.882493, 0.913806, 0.931949, 0.943785, 0.952125, ..., the smallest of which was found by Ramanujan (Berndt et al. ). 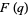 and its smallest positive root are related to the enumeration of coins in a fountain(Berndt 1991, Berndt et al. 1996, 2000) and the study of birth and death processes (Berndt et al. 1996, 2000; Parthasarathy et al. 1998). In general, the least positive root
and its smallest positive root are related to the enumeration of coins in a fountain(Berndt 1991, Berndt et al. 1996, 2000) and the study of birth and death processes (Berndt et al. 1996, 2000; Parthasarathy et al. 1998). In general, the least positive root 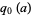 of
of 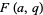 is given as
is given as  by
by
 |
(41) |
(OEIS A050203; Berndt et al. 1996, 2000). Ramanujan gave the amazing approximations
 |
 |
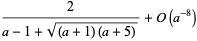 |
(42) |
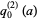 |
 |
![1/((a-1+sqrt((a+1)(a+5)))/2+[(a+3-sqrt((a+1)(a+5)))/(a-1+sqrt((a+1)(a+5)))]^3)+O(a^(-11)).](http://mathworld.wolfram.com/images/equations/Rogers-RamanujanContinuedFraction/Inline126.gif) |
(43) |
For 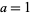 , these approximations give
, these approximations give
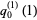 |
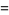 |
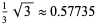 |
(44) |
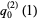 |
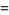 |
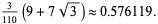 |
(45) |
More generally, for the broad class of 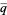 defined as
defined as 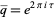 ,
, 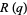 can be evaluated in terms of the j-function
can be evaluated in terms of the j-function 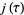 and the icosahedral equation as
and the icosahedral equation as
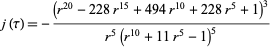 |
(46) |
with one of the 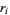 as
as 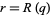 (Duke 2004). As an example,
(Duke 2004). As an example, 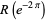 has
has 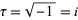 , so
, so 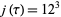 . Substituting
. Substituting 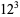 into the equation, one of its factors will be a quartic with the root
into the equation, one of its factors will be a quartic with the root 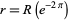 .
.
Furthermore, the numerator and the denominator (with a constant) can be combined to form a perfect square,
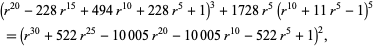 |
(47) |
which are in fact polynomial invariants of the icosahedral group.
REFERENCES:
Andrews, G. On the General Rogers-Ramanujan Theorem. Providence, RI: Amer. Math. Soc., 1974.
Andrews, G. E.; Berndt, B. C.; Jacobsen, L.; and Lamphere, R. L. The Continued Fractions Found in the Unorganized Portion of Ramanujan's Notebooks. Providence, RI: Amer. Math. Soc., 1992.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.
Berndt, B. C. Ramanujan's Notebooks, Part III. New York: Springer-Verlag, 1991.
Berndt, B. C. "Continued Fractions." Ch. 32 in Ramanujan's Notebooks, Part V. New York: Springer-Verlag, pp. 9-88, 1998.
Berndt, B. C. and Chan, H. H. "Some Values for the Rogers-Ramanujan Continued Fraction." Canad. J. Math. 47, 897-914, 1995.
Berndt, B. C. and Rankin, R. A. Ramanujan: Letters and Commentary. Providence, RI: Amer. Math. Soc, 1995.
Berndt, B. C.; Chan, H. H.; and Zhang, L.-C. "Explicit Evaluations of the Rogers-Ramanujan Continued Fraction." J. reine angew. Math. 480, 141-159, 1996.
Berndt, B. C.; Chan, H. H.; Huang, S.-S.; Kang, S.-Y.; Sohn, J.; and Son, S. H. "The Rogers-Ramanujan Continued Fraction." J. Comput. Appl. Math. 105, 9-24, 1999.
Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.
Duke, W. "Continued Fractions and Modular Functions." Bull. Amer. Math. Soc. 42, 137-162, 2005.
Joyce, G. S. "Exact Results for the Activity and Isothermal Compressibility of the Hard-Hexagon Model." J. Phys. A: Math. Gen. 21, L983-L988, 1988.
Parthasarathy, P. R.; Lenin, R. B.; Schoutens, W.; and van Assche, W. "A Birth and Death Process Related to the Rogers-Ramanujan Continued Fraction." J. Math. Anal. Appl. 224, 297-315, 1998.
Ramanathan, K. G. "On Ramanujan's Continued Fraction." Acta Arith. 43, 209-226, 1984a.
Ramanathan, K. G. "On the Rogers-Ramanujan Continued Fraction." Proc. Indian Acad. Sci. (Math. Sci.) 93, 67-77, 1984b.
Ramanathan, K. G. "Ramanujan's Continued Fraction." Indian J. Pure Appl. Math. 16, 695-724, 1985.
Ramanathan, K. G. "Some Applications of Kronecker's Limit Formula." J. Indian Math. Soc. 52, 71-89, 1987.
Ramanujan, S. Notebooks (2 Volumes). Bombay, India: Tata Institute, 1957.
Ramanujan, S. Collected Papers. New York: Chelsea, 1962.
Rogers, L. J. "Second Memoir on the Expansion of Certain Infinite Products." Proc. London Math. Soc. 25, 318-343, 1894.
Rogers, L. J. "On a Type of Modular Equations." Proc. London Math. Soc. 19, 387-397, 1920.
Sills, A. V. "Finite Rogers-Ramanujan Type Identities." Electron. J. Combin. 10, No. 13, 2003.
Sloane, N. J. A. Sequences A007325/M0415, A050203, A082682, A127836, and A128915 in "The On-Line Encyclopedia of Integer Sequences."
Son, S. H. "Some Theta Function Identities Related to the Rogers-Ramanujan Continued Fraction." Proc. Amer. Math. Soc. 126, 2895-2902, 1998.
Trott, M. "Modular Equations of the Rogers-Ramanujan Continued Fraction." Mathematica J. 9,314-333, 2004.
Watson, G. N. "Theorems Stated by Ramanujan (VII): Theorems on Continued Fractions." J. London Math. Soc. 4, 39-48, 1929a.
Watson, G. N. "Theorems Stated by Ramanujan (IX): Two Continued Fractions." J. London Math. Soc. 4, 231-237, 1929b.
Yi, J. "Evaluations of the Rogers-Ramanujan Continued Fraction 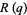 by Modular Equations." Acta Arith. 97, 103-127, 2001.
by Modular Equations." Acta Arith. 97, 103-127, 2001.
Yi, J. "Modular Equations for the Rogers-Ramanujan Continued Fraction and the Dedekind Eta-Function." Ramanujan J. 5, 377-384, 2002.