There are a great many beautiful identities involving 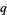-series, some of which follow directly by taking the q-analog of standard combinatorial identities, e.g., the q-binomial theorem

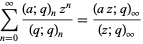(1)

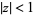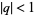(, ; Andrews 1986, p. 10), a special case of an identity due to Euler

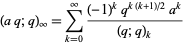(2)

(Gasper and Rahman 1990, p. 9; Leininger and Milne 1999), and q-Vandermonde sum

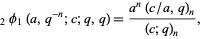(3)

where 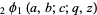 is a q-hypergeometric function.

Other 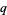-series identities, e.g., the Jacobi identities, Rogers-Ramanujan identities, and q-hypergeometric identity

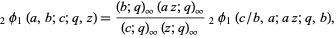(4)

seem to arise out of the blue. Another such example is

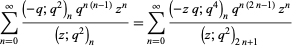(5)

(Gordon and McIntosh 2000).

Hirschhorn (1999) gives the beautiful identity

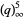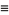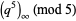			(6)
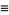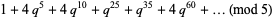			(7)

(OEIS A098445). Other modular identities involving the q-series 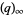 include

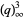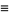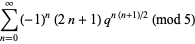			(8)
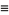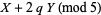			(9)

(Hardy and Wright 1979, Hirschhorn 1999), where

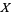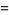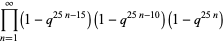			(10)
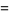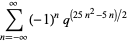			(11)
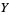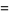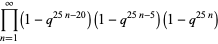			(12)
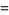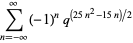			(13)

(Hirschhorn 1999).

Zucker (1990) defines the useful notations

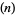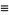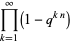			(14)
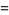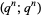			(15)
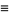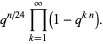			(16)

A set of beautiful identities that can be expressed in this notation were found by M. Trott (pers. comm., Dec. 19, 2000),

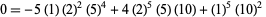	(17)
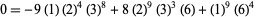	(18)
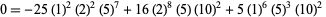	(19)
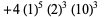	(20)
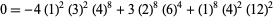	(21)
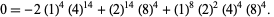	(22)

These are closely related to modular equation identities. For example, equation (◇) is an elegant form of Shen (1994) equation (3.12), obtained using the identities

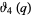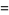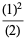			(23)
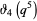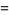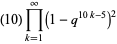			(24)
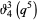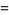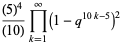			(25)

(OEIS A002448, A089803, and A089804). Similarly, equation (◇) is actually the classical expression

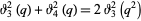(26)

for the Jacobi theta functions which follows from

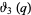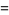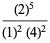			(27)
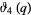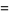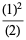			(28)

(J. Zucker, pers. comm., Nov. 11, 2003).

Another set of identities found by M. Trott (pers. comm., Jul. 8, 2009) are given by

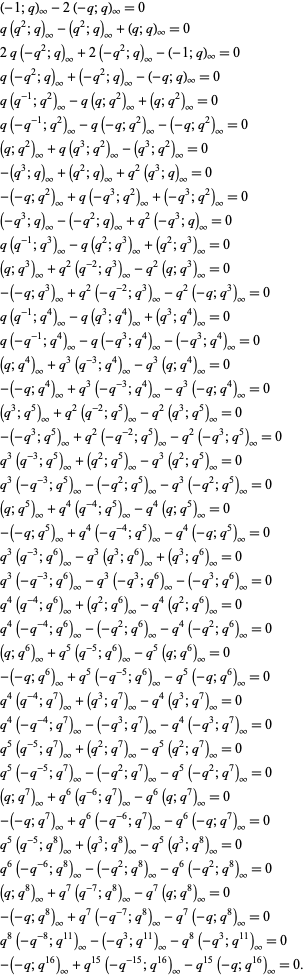(29)

REFERENCES:

Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.

Berndt, B. C. "Modular Equations of Degrees 3, 5, and 7 and Associated Theta-Function Identities." Ch. 19 in Ramanujan's Notebooks, Part III. New York:Springer-Verlag, pp. 220-324, 1985.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.

Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.

Leininger, V. E. and Milne, S. C. "Some New Infinite Families of 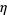-Function Identities." Methods Appl. Anal. 6, 225-248, 1999.

Shen, L.-C. "On the Additive Formulae of the Theta Functions and a Collection of Lambert Series Pertaining to the Modular Equations of Degree 5." Trans. Amer. Math. Soc. 345, 323-345, 1994.

Sloane, N. J. A. Sequences A002448, A089803, A089804, and A098445 in "The On-Line Encyclopedia of Integer Sequences."

Zucker, J. "Further Relations Amongst Infinite Series and Products. II. The Evaluation of Three-Dimensional Lattice Sums." J. Phys. A: Math. Gen. 23, 117-132, 1990.