A 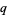-series is series involving coefficients of the form

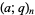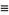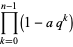			(1)
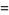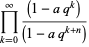			(2)
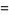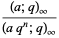			(3)

for 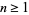, where  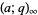is defined as

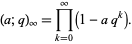(4)

The symbol 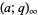 is called a q-Pochhammer symbol (Andrews 1986, p. 10) since it is a q-analog of the usual Pochhammer symbol. 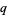-series obey beautifully sets of properties, and arise naturally in the theory of partitions, as well as in many problems of mathematical physics, especially those enumerating possible numbers of configurations or states on a lattice. The shorthand notation

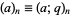(5)

is commonly encountered, and the notation

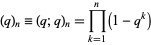(6)

is another special case (Hirschhorn 1999).

REFERENCES:

Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.

Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, 1998.

Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.

Berndt, B. C. "q-Series." Ch. 27 in Ramanujan's Notebooks, Part IV. New York:Springer-Verlag, pp. 261-286, 1994.

Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." To appears in Trans. Amer. Math. Soc.

Bhatnagar, G. "A Multivariable View of One-Variable q-Series." In Special Functions and Differential Equations. Proceedings of the Workshop (WSSF97) held in Madras, January 13-24, 1997) (Ed. K. S. Rao, R. Jagannathan, G. van den Berghe, and J. Van der Jeugt). New Delhi, India: Allied Pub., pp. 60-72, 1998.

Gasper, G. "Lecture Notes for an Introductory Minicourse on -Series." 25 Sep 1995. http://arxiv.org/abs/math.CA/9509223.

Gasper, G. "Elementary Derivations of Summation and Transformation Formulas for q-Series." In Fields Inst. Comm. 14 (Ed. M. E. H. Ismail et al. ), pp. 55-70, 1997.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.

Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.

Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 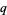-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.

Watson, G. N. "The Final Problem: An Account of the Mock Theta Functions." J. London Math. Soc. 11, 55-80, 1936.

Weisstein, E. W. "Books about q-Series." http://www.ericweisstein.com/encyclopedias/books/q-Series.html.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.