The q-analog of the Pochhammer symbol defined by

{product_(j=0)^(k-1)(1-aq^j) if k>0; 1 if k=0; product_(j=1)^(|k|)(1-aq^(-j))^(-1) if k<0; product_(j=0)^(infty)(1-aq^j) if k=infty " src="http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/NumberedEquation1.gif" style="height:182px; width:216px" />

(1)

(Koepf 1998, p. 25). -Pochhammer symbols are frequently called q-series and, for brevity, 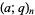 is often simply written 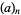. Note that this contention has the slightly curious side-effect that the argument is not taken literally, so for example  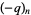means 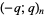, not 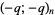 (cf. Andrews 1986b).

The 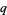-Pochhammer symbol  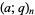is implemented in the Wolfram Language as QPochhammer[a, q, n], with the special cases  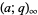and 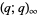 represented as QPochhammer[a, q] and QPochhammer[q], respectively.

Min Max

Min   Max       Re       Im

Letting 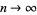 gives the special case , sometimes known as "the" Euler function 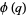 and defined by

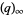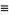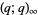			(2)
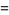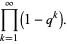			(3)

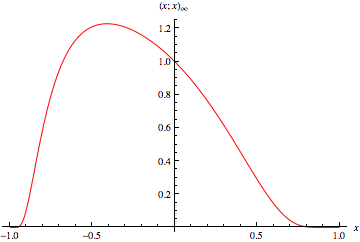
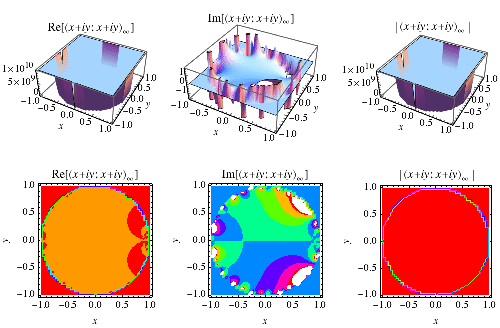
This function is closely related to the pentagonal number theorem and other related and beautiful sum/product identities. As mentioned above, it is implemented in Mathematica as QPochhammer[q]. As can be seen in the plot above, along the real axis, 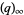reaches a maximum value  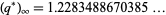(OEIS A143440) at value  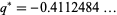(OEIS A143441).

The general 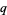-Pochhammer symbol is given by the sum

(4)

where  is a q-binomial coefficient (Koekoek and Swarttouw 1998, p. 11).

It is closely related to the Dedekind eta function,

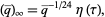(5)

where  the half-period ratio and 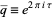 is the square of the nome (Berndt 1994, p. 139). Other representations in terms of special functions include

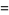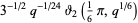			(6)
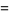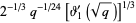			(7)

where 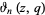 is a Jacobi theta function (and in the latter case, care must be taken with the definition of the principal value the cube root).

Asymptotic results for -Pochhammer symbols include

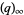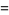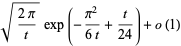			(8)
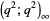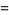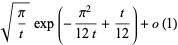			(9)
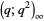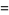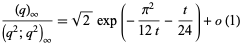			(10)

for 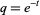 (Watson 1936, Gordon and McIntosh 2000).

For ,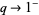

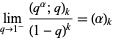(11)

gives the normal Pochhammer symbol 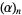 (Koekoek and Swarttouw 1998, p. 7). The 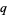-Pochhammer symbols are also called 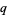-shifted factorials (Koekoek and Swarttouw 1998, pp. 8-9).

The 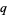-Pochhammer symbol satisfies

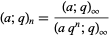(12)

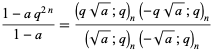(13)

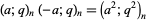(14)

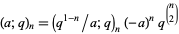(15)

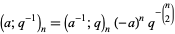(16)

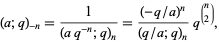(17)

(here, 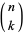 is a binomial coefficient so 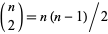), as well as many other identities, some of which are given by Koekoek and Swarttouw (1998, p. 9).

A generalized 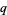-Pochhammer symbol can be defined using the concise notation

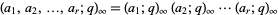(18)

(Gordon and McIntosh 2000).

The 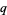-bracket

(19)

and 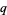-binomial

(20)

symbols are sometimes also used when discussing 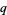-series, where  is a 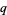-binomial coefficient.

REFERENCES:

Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986a.

Andrews, G. E. "The Fifth and Seventh Order Mock Theta Functions." Trans. Amer. Soc. 293, 113-134, 1986b.

Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, 1998.

Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.

Berndt, B. C. "q-Series." Ch. 27 in Ramanujan's Notebooks, Part IV. New York:Springer-Verlag, pp. 261-286, 1994.

Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.

Bhatnagar, G. "A Multivariable View of One-Variable q-Series." In Special Functions and Differential Equations. Proceedings of the Workshop (WSSF97) held in Madras, January 13-24, 1997) (Ed. K. S. Rao, R. Jagannathan, G. van den Berghe, and J. Van der Jeugt). New Delhi, India: Allied Pub., pp. 60-72, 1998.

Gasper, G. "Lecture Notes for an Introductory Minicourse on 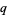-Series." 25 Sep 1995. http://arxiv.org/abs/math.CA/9509223.

Gasper, G. "Elementary Derivations of Summation and Transformation Formulas for q-Series." In Fields Inst. Comm. 14 (Ed. M. E. H. Ismail et al. ), pp. 55-70, 1997.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.

Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.

Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.

Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 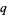-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 25 and 30, 1998.

Sloane, N. J. A. Sequences A143440 and A143441 in "The On-Line Encyclopedia of Integer Sequences."Watson, G. N. "The Final Problem: An Account of the Mock Theta Functions." J. London Math. Soc. 11, 55-80, 1936.