

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Jacobi Polynomial
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
4-8-2019
2113
The Jacobi polynomials, also known as hypergeometric polynomials, occur in the study of rotation groups and in the solution to the equations of motion of the symmetric top. They are solutions to the Jacobi differential equation, and give some other special named polynomials as special cases. They are implemented in the Wolfram Language as JacobiP[n, a, b, z].
For 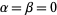 ,
, 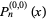 reduces to a Legendre polynomial. The Gegenbauer polynomial
reduces to a Legendre polynomial. The Gegenbauer polynomial
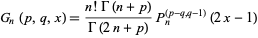 |
(1) |
and Chebyshev polynomial of the first kind can also be viewed as special cases of the Jacobi polynomials.
Plugging
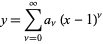 |
(2) |
into the Jacobi differential equation gives the recurrence relation
![[gamma-nu(nu+alpha+beta+1)]a_nu-2(nu+1)(nu+alpha+1)a_(nu+1)=0](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/NumberedEquation3.gif) |
(3) |
for 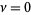 , 1, ..., where
, 1, ..., where
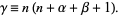 |
(4) |
Solving the recurrence relation gives
![P_n^((alpha,beta))(x)=((-1)^n)/(2^nn!)(1-x)^(-alpha)(1+x)^(-beta)(d^n)/(dx^n)[(1-x)^(alpha+n)(1+x)^(beta+n)]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/NumberedEquation5.gif) |
(5) |
for 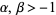 . They form a complete orthogonal system in the interval
. They form a complete orthogonal system in the interval ![[-1,1]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline5.gif) with respect to the weighting function
with respect to the weighting function
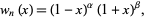 |
(6) |
and are normalized according to
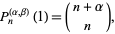 |
(7) |
where 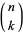 is a binomial coefficient. Jacobi polynomials can also be written
is a binomial coefficient. Jacobi polynomials can also be written
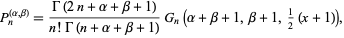 |
(8) |
where 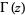 is the gamma function and
is the gamma function and
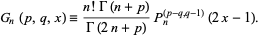 |
(9) |
Jacobi polynomials are orthogonal polynomials and satisfy
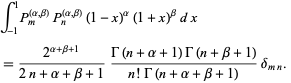 |
(10) |
The coefficient of the term 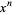 in
in 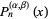 is given by
is given by
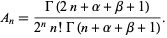 |
(11) |
They satisfy the recurrence relation
![2(n+1)(n+alpha+beta+1)(2n+alpha+beta)P_(n+1)^((alpha,beta))(x)
=[(2n+alpha+beta+1)(alpha^2-beta^2)+(2n+alpha+beta)_3x]P_n^((alpha,beta))(x)-2(n+alpha)(n+beta)(2n+alpha+beta+2)P_(n-1)^((alpha,beta))(x),](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/NumberedEquation12.gif) |
(12) |
where 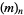 is a Pochhammer symbol
is a Pochhammer symbol
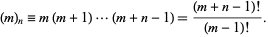 |
(13) |
The derivative is given by
![d/(dx)[P_n^((alpha,beta))(x)]=1/2(n+alpha+beta+1)P_(n-1)^((alpha+1,beta+1))(x).](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/NumberedEquation14.gif) |
(14) |
The orthogonal polynomials with weighting function 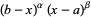 on the closed interval
on the closed interval ![[a,b]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline12.gif) can be expressed in the form
can be expressed in the form
![[const]P_n^((alpha,beta))(2(x-a)/(b-a)-1)](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/NumberedEquation15.gif) |
(15) |
(Szegö 1975, p. 58).
Special cases with 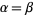 are
are
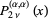 |
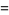 |
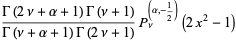 |
(16) |
 |
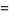 |
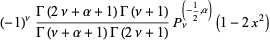 |
(17) |
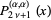 |
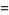 |
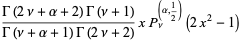 |
(18) |
 |
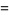 |
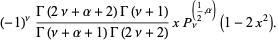 |
(19) |
Further identities are
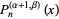 |
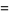 |
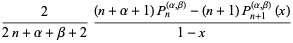 |
(20) |
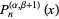 |
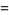 |
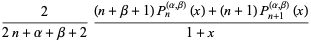 |
(21) |
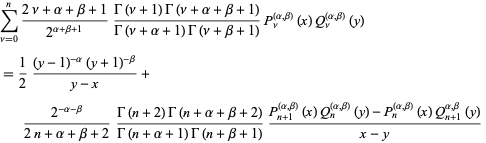 |
(22) |
(Szegö 1975, p. 79).
The kernel polynomial is
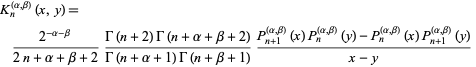 |
(23) |
(Szegö 1975, p. 71).
The polynomial discriminant is
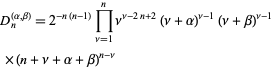 |
(24) |
(Szegö 1975, p. 143).
In terms of the hypergeometric function,
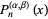 |
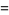 |
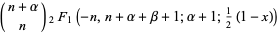 |
(25) |
 |
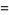 |
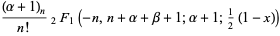 |
(26) |
 |
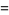 |
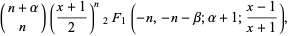 |
(27) |
where 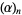 is the Pochhammer symbol (Abramowitz and Stegun 1972, p. 561; Koekoek and Swarttouw 1998).
is the Pochhammer symbol (Abramowitz and Stegun 1972, p. 561; Koekoek and Swarttouw 1998).
Let 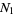 be the number of zeros in
be the number of zeros in 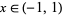 ,
, 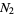 the number of zeros in
the number of zeros in 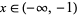 , and
, and 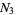 the number of zeros in
the number of zeros in 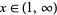 . Define Klein's symbol
. Define Klein's symbol
|
(28) |
where 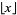 is the floor function, and
is the floor function, and
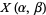 |
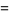 |
![E[1/2(|2n+alpha+beta+1|-|alpha|-|beta|+1)]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline51.gif) |
(29) |
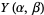 |
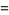 |
![E[1/2(-|2n+alpha+beta+1|+|alpha|-|beta|+1)]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline54.gif) |
(30) |
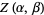 |
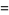 |
![E[1/2(-|2n+alpha+beta+1|-|alpha|+|beta|+1)].](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline57.gif) |
(31) |
If the cases 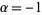 ,
, 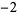 , ...,
, ..., 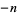 ,
, 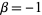 ,
, 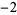 , ...,
, ..., 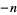 , and
, and 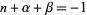 ,
, 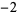 , ...,
, ..., 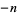 are excluded, then the number of zeros of
are excluded, then the number of zeros of 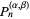 in the respective intervals are
in the respective intervals are
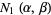 |
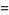 |
(32) |
|
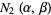 |
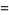 |
(33) |
|
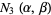 |
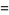 |
(34) |
(Szegö 1975, pp. 144-146), where 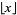 is again the floor function.
is again the floor function.
The first few polynomials are
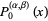 |
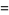 |
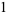 |
(35) |
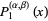 |
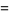 |
![1/2[2(alpha+1)+(alpha+beta+2)(x-1)]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline83.gif) |
(36) |
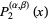 |
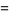 |
![1/8[4(alpha+1)(alpha+2)+4(alpha+beta+3)(alpha+2)(x-1)+(alpha+beta+3)(alpha+beta+4)(x-1)^2]](http://mathworld.wolfram.com/images/equations/JacobiPolynomial/Inline86.gif) |
(37) |
(Abramowitz and Stegun 1972, p. 793).
See Abramowitz and Stegun (1972, pp. 782-793) and Szegö (1975, Ch. 4) for additional identities.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.
Andrews, G. E.; Askey, R.; and Roy, R. "Jacobi Polynomials and Gram Determinants" and "Generating Functions for Jacobi Polynomials." §6.3 and 6.4 in Special Functions. Cambridge, England: Cambridge University Press, pp. 293-306, 1999.
Iyanaga, S. and Kawada, Y. (Eds.). "Jacobi Polynomials." Appendix A, Table 20.V in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1480, 1980.
Koekoek, R. and Swarttouw, R. F. "Jacobi." §1.8 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 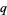 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 38-44, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 38-44, 1998.
Roman, S. "The Theory of the Umbral Calculus I." J. Math. Anal. Appl. 87, 58-115, 1982.
Szegö, G. "Jacobi Polynomials." Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.