

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Logarithmic Integral
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
1-8-2019
2139
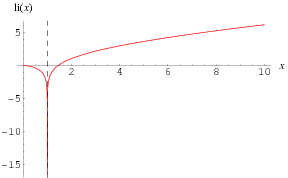
The logarithmic integral (in the "American" convention; Abramowitz and Stegun 1972; Edwards 2001, p. 26), is defined for real  as
as
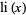 |
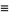 |
(1) |
|
 |
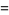 |
(2) |
Here, PV denotes Cauchy principal value of the integral, and the function has a singularity at 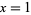 .
.
The logarithmic integral defined in this way is implemented in the Wolfram Language as LogIntegral[x].
There is a unique positive number
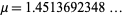 |
(3) |
(OEIS A070769; Derbyshire 2004, p. 114) known as Soldner's constant for which 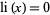 , so the logarithmic integral can also be written as
, so the logarithmic integral can also be written as
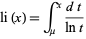 |
(4) |
for 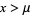 .
.
Special values include
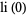 |
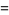 |
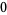 |
(5) |
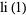 |
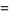 |
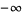 |
(6) |
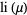 |
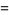 |
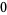 |
(7) |
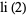 |
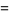 |
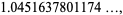 |
(8) |
(OEIS A069284), where 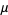 is Soldner's constant (Edwards 2001, p. 34).
is Soldner's constant (Edwards 2001, p. 34).
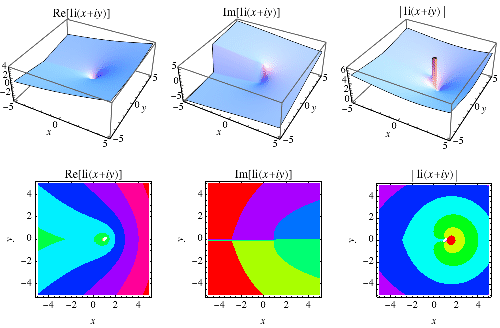 |
The definition can also be extended to the complex plane, as illustrated above.
Its derivative is
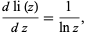 |
(9) |
and its indefinite integral is
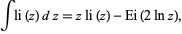 |
(10) |
where 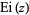 is the exponential integral. It also has the definite integral
is the exponential integral. It also has the definite integral
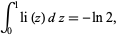 |
(11) |
where 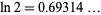 (OEIS A002162) is the natural logarithm of 2.
(OEIS A002162) is the natural logarithm of 2.
The logarithmic integral obeys
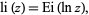 |
(12) |
where 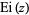 is the exponential integral, as well as the identity
is the exponential integral, as well as the identity
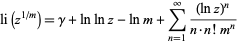 |
(13) |
(Bromwich and MacRobert 1991, p. 334; Hardy 1999, p. 25).
Nielsen showed and Ramanujan independently discovered that
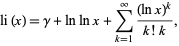 |
(14) |
where 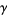 is the Euler-Mascheroni constant (Nielsen 1965, pp. 3 and 11; Berndt 1994; Finch 2003; Havil 2003, p. 106). Another formula due to Ramanujan which converges more rapidly is
is the Euler-Mascheroni constant (Nielsen 1965, pp. 3 and 11; Berndt 1994; Finch 2003; Havil 2003, p. 106). Another formula due to Ramanujan which converges more rapidly is
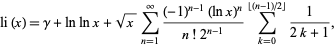 |
(15) |
where 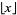 is the floor function (Berndt 1994).
is the floor function (Berndt 1994).
The form of this function appearing in the prime number theorem (used for example by Landau as well as Havil 2003, pp. 105 and 175) and sometimes referred to as the "European" definition (Derbyshire 2004, p. 373) is defined so that 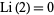 :
:
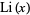 |
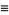 |
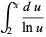 |
(16) |
 |
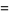 |
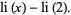 |
(17) |
Note that the notation 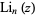 is (confusingly) also used for the polylogarithm and also for the "American" definition of
is (confusingly) also used for the polylogarithm and also for the "American" definition of 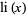 (Edwards 2001, p. 26).
(Edwards 2001, p. 26).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 879, 1972.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 126-131, 1994.
Bromwich, T. J. I'A. and MacRobert, T. M. An Introduction to the Theory of Infinite Series, 3rd ed. New York: Chelsea, p. 334, 1991.
de Morgan, A. The Differential and Integral Calculus, Containing Differentiation, Integration, Development, Series, Differential Equations, Differences, Summation, Equations of Differences, Calculus of Variations, Definite Integrals--With Applications to Algebra, Plane Geometry, Solid Geometry, and Mechanics. London: Robert Baldwin, p. 662, 1839.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 114-117 and 373, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Finch, S. R. "Euler-Gompertz Constant." §6.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 423-428, 2003.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 105-106 and 175-176, 2003.
Koosis, P. The Logarithmic Integral I. Cambridge, England: Cambridge University Press, 1998.
Nielsen, N. "Theorie des Integrallograrithmus und Verwandter Transzendenten." Part II in Die Gammafunktion. New York: Chelsea, 1965.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 151, 1991.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 45, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 39, 1983.
Sloane, N. J. A. Sequences A0021624074, A069284 and A070769 in "The On-Line Encyclopedia of Integer Sequences."
Soldner. Abhandlungen 2, 333, 1812.