The power tower of order 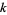 is defined as

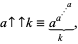(1)

where  is Knuth up-arrow notation (Knuth 1976), which in turn is defined by

(2)

together with

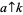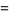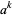			(3)
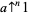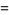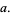			(4)

Rucker (1995, p. 74) uses the notation

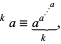(5)

and refers to this operation as "tetration."

A power tower can be implemented in the Wolfram Language as

  PowerTower[a_, k_Integer] := Nest[Power[a, #]&, 1, k]

or

  PowerTower[a_, k_Integer] := Power @@ Table[a, {k}]

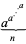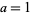The following table gives values of  for , 2, ... for small .

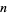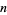	Sloane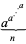
1	A000027	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...
2	A000312	1, 4, 27, 256, 3125, 46656, ...
3	A002488	1, 16, 7625597484987, ...
4		1, 65536, ...

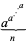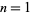The following table gives  for , 2, ... for small .

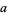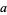	Sloane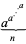
1	A000012	1, 1, 1, 1, 1, 1, ...
2	A014221	2, 4, 16, 65536, , ...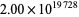
3	A014222	3, 27, 7625597484987, ...
4		4, 256, , ...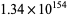

Consider 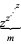 and let  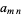be defined as

{1 if n=0; 1/(n!) if m=1; 1/nsum_(j=1)^(n)ja_(m,n-j)a_(m-1,j-1) otherwise " src="http://mathworld.wolfram.com/images/equations/PowerTower/NumberedEquation4.gif" style="height:114px; width:242px" />

(6)

(Galidakis 2004). Then for 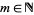,  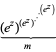is entire with series expansion:

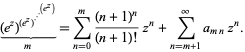(7)

Similarly, for 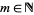,  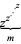is analytic for  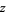in the domain of the principal branch of 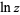, with series expansion:

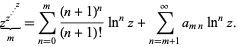(8)

For 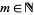, and ,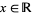

(9)

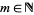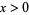For , and , and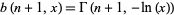 

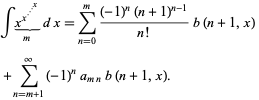(10)

Min Max

Min   Max       Re       Im

The value of the infinite power tower 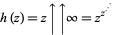, where  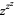is an abbreviation for 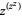, can be computed analytically by writing

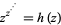(11)

taking the logarithm of both sides and plugging back in to obtain

(12)

Solving for 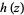 gives

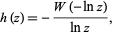(13)

where 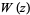 is the Lambert W-function (Corless et al. 1996).  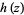converges iff  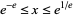(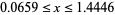; OEIS A073230 and A073229), as shown by Euler (1783) and Eisenstein (1844) (Le Lionnais 1983; Wells 1986, p. 35).

Knoebel (1981) gave the following series for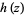 

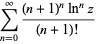			(14)
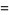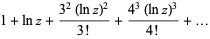			(15)

(Vardi 1991).

The special value 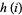 is given by

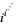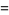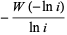			(16)
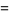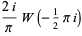			(17)
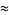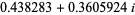			(18)

(OEIS A077589 and A077590; Macintyre 1966).

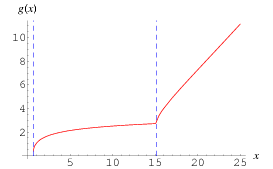
The related function

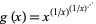(19)

converges only for 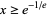, that is,  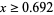(OEIS A072364). The value it converges to is the inverse of  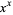which can be found by taking the logarithm of both sides of (19),

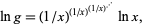(20)

rearranging to

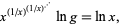(21)

and then substituting to obtain

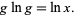(22)

Solving the resulting equation for  then gives the partial solution

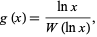(23)

which is valid for 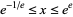 (i.e., 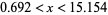; OEIS A072364 and A073226). Taking  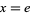then gives 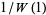, where  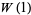is the omega constant.

A continued fraction due to Khovanskii (1963) for the single iteration of 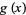 is given by

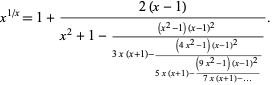(24)

Min Max

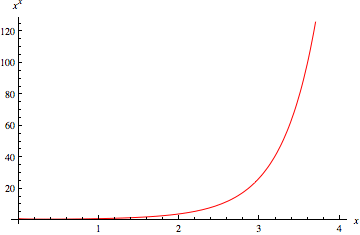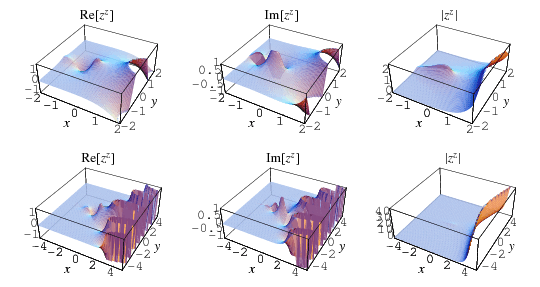
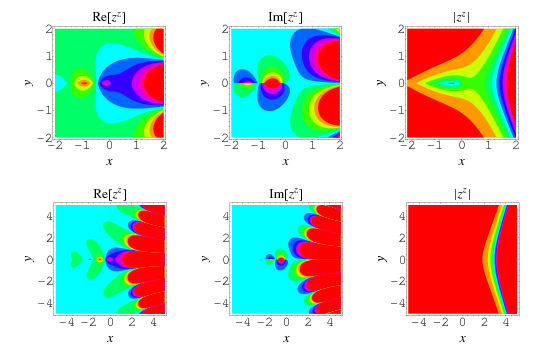
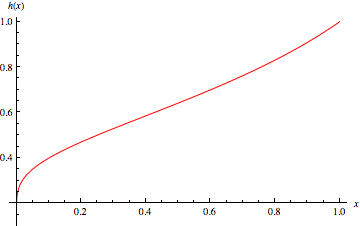
The function 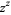 is plotted above along the real line and in the complex plane. It has series expansion

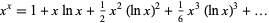(25)

(Trott 2004, p. 59). It has a minimum where

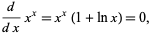(26)

which has solution 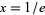. At this point, the function takes on the value .

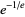The indefinite integral

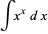(27)

cannot be expressed in terms of a finite number of elementary functions, but some interesting definite integrals of 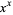are

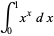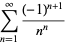			(28)
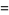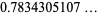			(29)
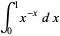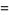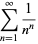			(30)
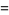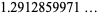			(31)

(OEIS A083648 and A073009; Spiegel 1968; Abramowitz and Stegun 1972; Havil 2003, pp. 44-45; Borwein et al. 2004, p. 5). Borwein et al. (2004, pp. 5 and 44) call these two integrals "a sophomore's dream."

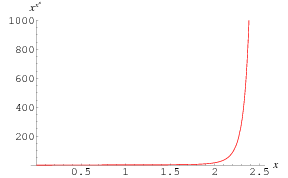
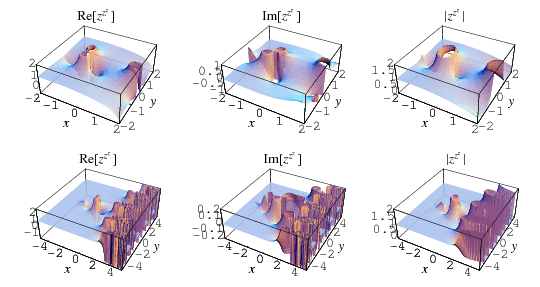
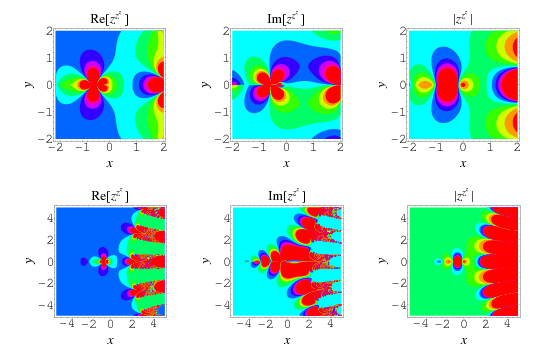
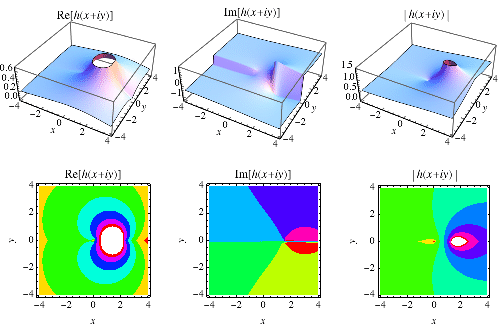
The function 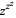 is plotted above along the real line and in the complex plane, where it shows beautiful structure.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

Ash, J. M. "The Limit of 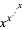 as  Tends to Infinity." Math. Mag. 69, 207-209, 1996.

Baker, I. N. and Rippon, P. J. "Convergence of Infinite Exponentials." Ann. Acad. Sci. Fennicæ Ser. A. I. Math. 8, 179-186, 1983.

Baker, I. N. and Rippon, P. J. "Iteration of Exponential Functions." Ann. Acad. Sci. Fennicæ Ser. A. I. Math. 9, 49-77, 1984.

Baker, I. N. and Rippon, P. J. "A Note on Complex Iteration." Amer. Math. Monthly 92, 501-504, 1985.

Barrow, D. F. "Infinite Exponentials." Amer. Math. Monthly 43, 150-160, 1936.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 61-62, 2004.

Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; and Knuth, D. E. "On the Lambert 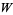 Function." Adv. Comput. Math.5, 329-359, 1996.

Creutz, M. and Sternheimer, R. M. "On the Convergence of Iterated Exponentiation, Part I." Fib. Quart. 18, 341-347, 1980.

Creutz, M. and Sternheimer, R. M. "On the Convergence of Iterated Exponentiation, Part II." Fib. Quart. 19, 326-335, 1981.

de Villiers, J. M. and Robinson, P. N. "The Interval of Convergence and Limiting Functions of a Hyperpower Sequence." Amer. Math. Monthly 93, 13-23, 1986.

Eisenstein, G. "Entwicklung von 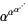." J. reine angew. Math. 28, 49-52, 1844.

Elstrodt, J. "Iterierte Potenzen." Math. Semesterber. 41, 167-178, 1994.

Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29-51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. pp. 350-369.

Finch, S. R. "Iterated Exponential Constants." §6.11 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 448-452, 2003.

Galidakis, I. N. "On An Application of Lambert's 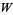 Function to Infinite Exponentials." Complex Variables Th. Appl. 49, 759-780, 2004.

Ginsburg, J. "Iterated Exponentials." Scripta Math. 11, 340-353, 1945.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Khovanskii, A. N. The Application of Continued Fractions and Their Generalizations to Problems in Approximation Theory.Groningen, Netherlands: P. Noordhoff, 1963.

Knoebel, R. A. "Exponentials Reiterated." Amer. Math. Monthly 88, 235-252, 1981.

Knuth, D. E. "Mathematics and Computer Science: Coping with Finiteness. Advances in our Ability to Compute are Bringing us Substantially Closer to Ultimate Limitations." Science 194, 1235-1242, 1976.

Länger, H. "An Elementary Proof of the Convergence of Iterated Exponentials." Elem. Math. 51, 75-77, 1996.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 22 and 39, 1983.

Macdonnell, J. "Some Critical Points on the Hyperpower Function 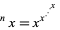." Int. J. Math. Educ. Sci. Technol. 20, 297-305, 1989.

Macintyre, A. J. "Convergence of 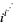." Proc. Amer. Math. Soc. 17, 67, 1966.

Mauerer, H. "Über die Funktion 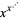 für ganzzahliges Argument (Abundanzen)." Mitt. Math. Gesell. Hamburg 4, 33-50, 1901.

Meyerson, M. D. "The 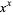 Spindle." Math. Mag. 69, 198-206, 1996.

Rippon, P. J. "Infinite Exponentials." Math. Gaz. 67, 189-196, 1983.

Rucker, R. Infinity and the Mind: The Science and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1995.

Sloane, N. J. A. Sequences A072364, A073226, A073229, A073230, A077589, A077590, A083648, and A073009 in "The On-Line Encyclopedia of Integer Sequences."

Spiegel, M. R. Mathematical Handbook of Formulas and Tables. New York: McGraw-Hill, 1968.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 11-12 and 226-229, 1991.

Weber, R. O. and Roumeliotis, J. "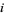^^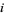^^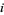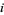...." Austral. Math. Soc. Gaz. 22, 182-184, 1995.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 35, 1986.