The Mathieu functions are the solutions to the Mathieu differential equation

(1)

Even solutions are denoted 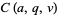 and odd solutions by 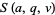. These are returned by the Wolfram Language functions MathieuC[a, q, z] and MathieuS[a, q, z], respectively. Similarly, their derivatives are implemented as MathieuCPrime[a, q, z] and MathieuSPrime[a, q, z].

These functions appear in physical problems involving elliptical shapes or periodic potentials, and were first introduced by Mathieu (1868) when analyzing the motion of elliptical membranes. Unfortunately, the analytic determination of Mathieu functions "presents great difficulties" (Whittaker 1914, Frenkel and Portugal 2001), and they are difficult to employ, "mainly because of the impossibility of analytically representing them in a simple and handy way" (Sips 1949, Frenkel and Portugal 2001).

The Mathieu functions have the special values

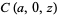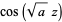			(2)
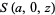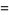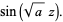			(3)

For nonzero 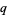, the Mathieu functions are only periodic in  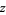for certain values of 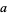. Such characteristic values are given by the Wolfram Language functions MathieuCharacteristicA[r, q] and MathieuCharacteristicB[r, q] with  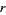an integer or rational number. These values are often denote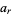d  and 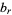. In general, both  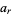and 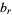 are multivalued functions with very complicated branch cut structures. Unfortunately, there is no general agreement on how to define the branch cuts. As a result, the Wolfram Language's implementation simply picks a convenient sheet.

For integer 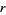, the even and odd Mathieu functions with characteristic values  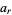and 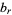 are often denote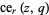d  and 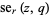, known as the elliptic cosine and elliptic sine functions, respectively (Abramowitz and Stegun 1972, p. 725; Frenkel and Portugal 2001). The left plot above shows  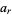for 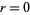, 1, ..., 4 and the right plot shows  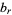for 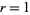, ..., 4.

Whittaker and Watson (1990, p. 405) define the Mathieu function based on the equation

(4)

This equation is closely related to Hill's differential equation. For an even Mathieu function,

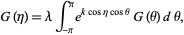(5)

where 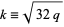. For an odd Mathieu function,

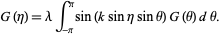(6)

Both even and odd functions satisfy

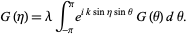(7)

Letting 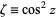 transforms the Mathieu differential equation to

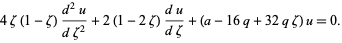(8)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Mathieu Functions." Ch. 20 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 721-746, 1972.

Blanch, G. "Asymptotic Expansion for the Odd Periodic Mathieu Functions." Trans. Amer. Math. Soc. 97, 357-366, 1960.

Dingle, R. B. and Müller, H. J. W. "Asymptotic Expansions of Mathieu Functions and Their Characteristic Numbers." J. reine angew. Math. 211, 11-32, 1962.

Frenkel, D. and Portugal, R. "Algebraic Methods to Compute Mathieu Functions." J. Phys. A: Math. Gen. 34, 3541-3551, 2001.

Gradshteyn, I. S. and Ryzhik, I. M. "Mathieu Functions." §6.9 and 8.6 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 800-804 and 1006-1013, 2000.

Humbert, P. Fonctions de Lamé et Fonctions de Mathieu. Paris: Gauthier-Villars, 1926.

Mathieu, É. "Mémoire sur le mouvement vibratoire d'une membrane de forme elliptique." J. math. pure appl. 13, 137-203, 1868.

McLachlan, N. W. Theory and Applications of Mathieu Functions. New York: Dover, 1964.

Mechel, F. P. Mathieu Functions: Formulas, Generation, Use. Stuttgart, Germany: Hirzel, 1997.

Meixner, J. and Schäfke, F. W. Mathieusche Funktionen und Sphäroidfunktionen. Berlin: Springer-Verlag, 1954.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 562-568 and 633-642, 1953.

Rubin, H. "Anecdote on Power Series Expansions of Mathieu Functions." J. Math. Phys. 43, 339-341, 1964.

Sips, R. "Représentation asymptotique des fonctions de Mathieu et des fonctions d'onde sphéroidales." Trans. Amer. Math. Soc. 66, 93-134, 1949.

Whittaker, E. T. "On the General Solution of Mathieu's Equation." Proc. Edinburgh Math. Soc. 32, 75-80, 1914.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.