

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Modified Bessel Function of the Second Kind
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Modified Bessel Functions I and K." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
25-3-2019
4516

The modified bessel function of the second kind is the function 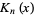 which is one of the solutions to the modified Bessel differential equation. The modified Bessel functions of the second kind are sometimes called the Basset functions, modified Bessel functions of the third kind (Spanier and Oldham 1987, p. 499), or Macdonald functions (Spanier and Oldham 1987, p. 499; Samko et al. 1993, p. 20). The modified Bessel function of the second kind is implemented in the Wolfram Language as BesselK[nu, z].
which is one of the solutions to the modified Bessel differential equation. The modified Bessel functions of the second kind are sometimes called the Basset functions, modified Bessel functions of the third kind (Spanier and Oldham 1987, p. 499), or Macdonald functions (Spanier and Oldham 1987, p. 499; Samko et al. 1993, p. 20). The modified Bessel function of the second kind is implemented in the Wolfram Language as BesselK[nu, z].
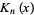 is closely related to the modified Bessel function of the first kind
is closely related to the modified Bessel function of the first kind 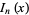 and Hankel function
and Hankel function 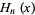 ,
,
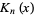 |
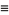 |
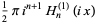 |
(1) |
 |
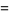 |
![1/2pii^(n+1)[J_n(ix)+iN_n(ix)]](http://mathworld.wolfram.com/images/equations/ModifiedBesselFunctionoftheSecondKind/Inline10.gif) |
(2) |
 |
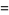 |
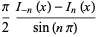 |
(3) |
(Watson 1966, p. 185). A sum formula for 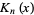 is
is
^k)/(k!(n+k)!),](http://mathworld.wolfram.com/images/equations/ModifiedBesselFunctionoftheSecondKind/NumberedEquation1.gif) |
(4) |
where 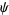 is the digamma function (Abramowitz and Stegun 1972). An integral formula is
is the digamma function (Abramowitz and Stegun 1972). An integral formula is
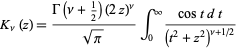 |
(5) |
which, for 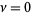 , simplifies to
, simplifies to
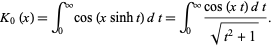 |
(6) |
Other identities are
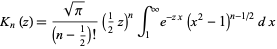 |
(7) |
for 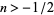 and
and
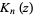 |
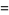 |
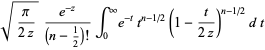 |
(8) |
 |
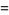 |
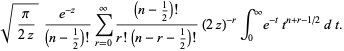 |
(9) |

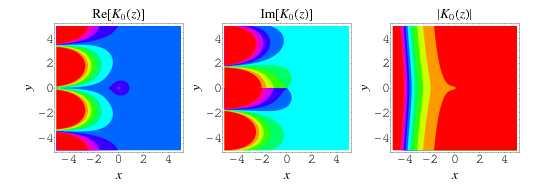
The special case of 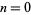 gives
gives 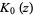 as the integrals
as the integrals
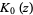 |
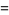 |
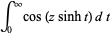 |
(10) |
 |
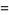 |
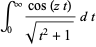 |
(11) |
(Abramowitz and Stegun 1972, p. 376).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Bessel Functions 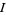 and
and 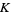 ." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.
." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.
Arfken, G. "Modified Bessel Functions, 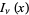 and
and 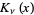 ." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Modified Bessel Functions of Integral Order" and "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.6 and 6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 229-245, 1992.
Samko, S. G.; Kilbas, A. A.; and Marichev, O. I. Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, p. 20, 1993.
Spanier, J. and Oldham, K. B. "The Basset 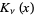 ." Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
." Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.