
Branch Cut
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
andbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
andbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 27-11-2018
27-11-2018
 1849
1849
Branch Cut
A branch cut is a curve (with ends possibly open, closed, or half-open) in the complex plane across which an analytic multivalued function is discontinuous. For convenience, branch cuts are often taken as lines or line segments. Branch cuts (even those consisting of curves) are also known as cut lines (Arfken 1985, p. 397), slits (Kahan 1987), or branch lines.
For example, consider the function 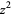 which maps each complex number
which maps each complex number 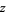 to a well-defined number
to a well-defined number 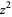 . Its inverse function
. Its inverse function 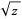 , on the other hand, maps, for example, the value
, on the other hand, maps, for example, the value 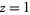 to
to 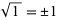 . While a unique principal value can be chosen for such functions (in this case, the principal square root is the positive one), the choices cannot be made continuous over the whole complex plane. Instead, lines of discontinuity must occur. The most common approach for dealing with these discontinuities is the adoption of so-called branch cuts. In general, branch cuts are not unique, but are instead chosen by convention to give simple analytic properties (Kahan 1987). Some functions have a relatively simple branch cut structure, while branch cuts for other functions are extremely complicated.
. While a unique principal value can be chosen for such functions (in this case, the principal square root is the positive one), the choices cannot be made continuous over the whole complex plane. Instead, lines of discontinuity must occur. The most common approach for dealing with these discontinuities is the adoption of so-called branch cuts. In general, branch cuts are not unique, but are instead chosen by convention to give simple analytic properties (Kahan 1987). Some functions have a relatively simple branch cut structure, while branch cuts for other functions are extremely complicated.
An alternative to branch cuts for representing multivalued functions is the use of Riemann surfaces.
In addition to branch cuts, singularities known as branch points also exist. It should be noted, however, that the endpoints of branch cuts are not necessarily branch points.
Branch cuts do not arise for the single-valued trigonometric, hyperbolic, integer power, and exponential functions. However, their multivalued inverses do require branch cuts. The plots and table below summarize the branch cut structure of inverse trigonometric, inverse hyperbolic, noninteger power, and logarithmic functions adopted in the Wolfram Language.
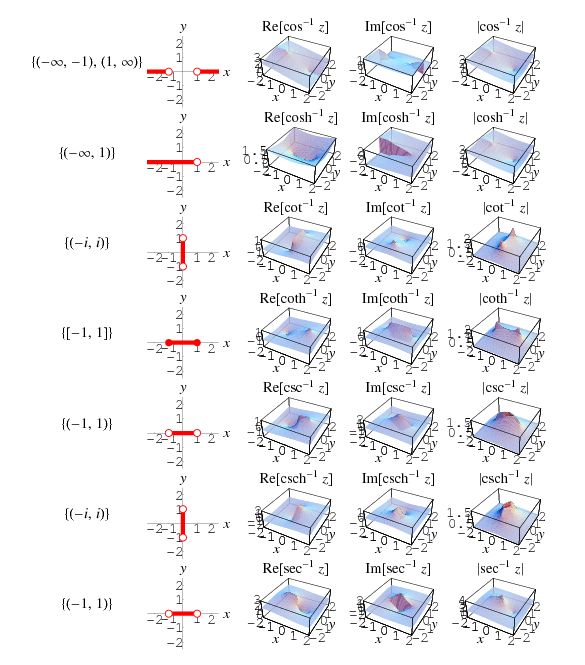
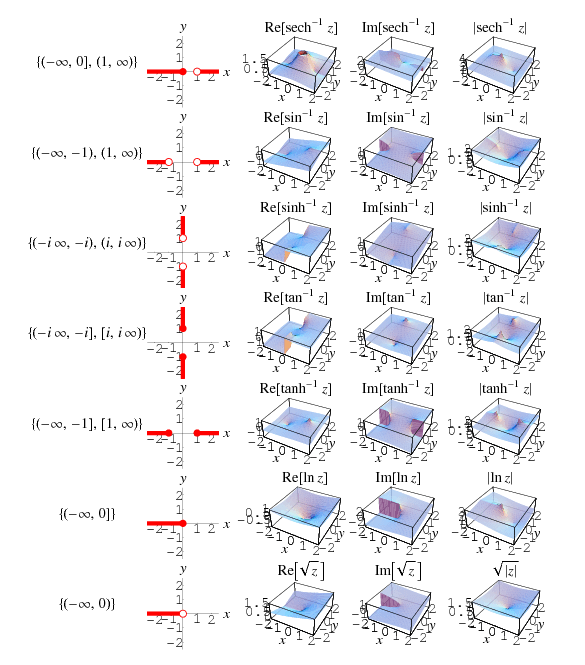
| function name |
function |
branch cut(s) |
| inverse cosecant |
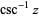 |
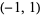 |
| inverse cosine |
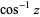 |
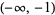 and and 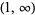 |
| inverse cotangent |
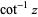 |
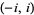 |
| inverse hyperbolic cosecant |
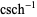 |
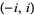 |
| inverse hyperbolic cosine |
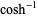 |
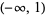 |
| inverse hyperbolic cotangent |
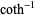 |
![[-1,1]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline19.gif) |
| inverse hyperbolic secant |
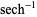 |
![(-infty,0]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline21.gif) and and 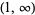 |
| inverse hyperbolic sine |
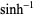 |
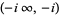 and and 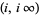 |
| inverse hyperbolic tangent |
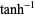 |
![(-infty,-1]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline27.gif) and and 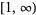 |
| inverse secant |
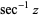 |
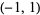 |
| inverse sine |
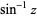 |
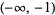 and and 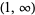 |
| inverse tangent |
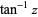 |
![(-iinfty,-i]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline35.gif) and and 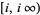 |
| natural logarithm |
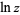 |
![(-infty,0]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline38.gif) |
| power |
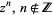 |
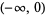 for for ![R[n]<=0](http://mathworld.wolfram.com/images/equations/BranchCut/Inline41.gif) ; ; ![(-infty,0]](http://mathworld.wolfram.com/images/equations/BranchCut/Inline42.gif) for for ![R[n]>0](http://mathworld.wolfram.com/images/equations/BranchCut/Inline43.gif) |
| square root |
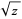 |
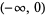 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79 and 86, 1972.
Ahlfors, L. V. Complex Analysis, 3rd ed. New York: McGraw-Hill, p. 75, 1979.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Bradford, R.; Corless, R. M.; Davenport, J. H.; Jeffrey, D. J.; and Watt, S. M. "Reasoning About the Elementary Functions of Complex Analysis." Ann. Math. Artificial Intell. 36, 303-318, 2002.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, 1997.
Dingle, A. and Fateman, R. J. "Branch Cuts in Computer Algebra." In Symbolic and Algebraic Computation (Ed. J. von zur Gathen and M. Giesbracht). New York: ACM Press, pp. 250-257, 1994.
Duffy, D. G. Transform Methods for Solving Partial Differential Equations, 2nd ed. Boca Raton, FL: CRC Press, 2004.
Felsen, L. B. and Marcuvitz, I. N. Radiation and Scattering of Waves. New York: IEEE Press, 1994.
Kahan, W. "Branch Cuts for Complex Elementary Functions, or Much Ado About Nothing's Sign Bit." In The State of the Art in Numerical Analysis: Proceedings of the Joint IMA/SIAM Conference on the State of the Art in Numerical Analysis Held at the UN (Ed. A. Iserles and M. J. D. Powell). New York: Clarendon Press, pp. 165-211, 1987.
Korn, G. A. and Korn, T. M. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill, 1968.
Mahan, G. D. Applied Mathematics. New York: Kluwer, 2002.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 399-401, 1953.
Remmert, R. Funktionentheorie 1. Berlin: Springer-Verlag, 1992.
Remmert, R. Funktionentheorie 2. Berlin: Springer-Verlag, 1992.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 188-191, 2004. http://www.mathematicaguidebooks.org/.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


