Variation of Argument
المؤلف:
Barnard, R. W.; Dayawansa, W.; Pearce, K.; and Weinberg, D
المصدر:
"Polynomials with Nonnegative Coefficients." Proc. Amer. Math. Soc. 113
الجزء والصفحة:
77-83
17-11-2018
729
Variation of Argument
Let ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline1.gif)
denote the change in the complex argument of a function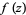 
around a contour 
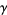. Also let 
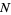denote the number of roots of 
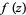in 
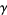and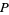 
denote the sum of the orders of all poles of 
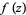lying inside 
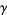. Then
![[arg(f(z))]=2pi(N-P).](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation1.gif) |
(1)
|
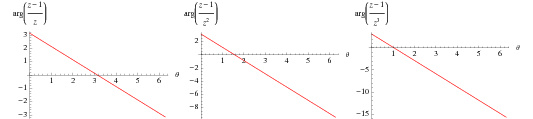
For example, the plots above shows the argument for a small circular contour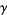 
centered around 
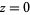for a function of the form 
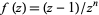(which has a single pole of order 
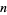and no roots in 
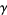) for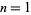 
, 2, and 3.
Note that the complex argument must change continuously, so any "jumps" that occur as the contour crosses branch cuts must be taken into account.
To find ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline16.gif)
in a given region 
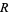, break 
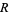into paths and find ![[arg(f(z))]](http://mathworld.wolfram.com/images/equations/VariationofArgument/Inline19.gif)
for each path. On a circular arc
 |
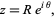(2)
|
let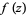 
be a polynomial 
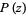of degree 
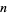. Then
Plugging in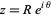 
gives
![[arg(P(z))]=[arg(Re^(ithetan))]+[arg((P(Re^(itheta)))/(Re^(ithetan)))].](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation3.gif) |
(5)
|
So as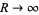 
,
![lim_(R->infty)(P(Re^(itheta)))/(Re^(ithetan))=[constant]](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation4.gif) |
(6)
|
![[(P(Re^(itheta)))/(Re^(ithetan))]=0,](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation5.gif) |
(7)
|
and
![[arg(P(z))]=[arg(e^(ithetan))]=n(theta_2-theta_1).](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation6.gif) |
(8)
|
For a real segment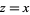 
,
![[arg(f(x))]=tan^(-1)[0/(f(x))]=0.](http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation7.gif) |
(9)
|
For an imaginary segment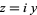 
,
![[arg(f(iy))]=<span style=]() {tan^(-1)(I[P(iy)])/(R[P(iy)])}_(theta_1)^(theta_2). " src="http://mathworld.wolfram.com/images/equations/VariationofArgument/NumberedEquation8.gif" style="height:38px; width:213px" /> |
(10)
|
REFERENCES:
Barnard, R. W.; Dayawansa, W.; Pearce, K.; and Weinberg, D. "Polynomials with Nonnegative Coefficients." Proc. Amer. Math. Soc. 113, 77-83, 1991.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
