Although Descartes originally used the term "imaginary number" to refer to what is today known as a complex number, in standard usage today, "imaginary number" means a complex number 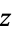 that has zero real part (i.e., such that ). For clarity, such numbers are perhaps best referred to as purely imaginary numbers.

A (purely) imaginary number can be written as a real number multiplied by the "imaginary unit" i (equal to the square root 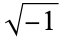), i.e., in the form .

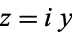In the novel The Da Vinci Code, the character Robert Langdon jokes that character Sophie Neveu "believes in the imaginary number 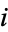 because it helps her break code" (Brown 2003, p. 351). In Isaac Asimov's short story "The Imaginary" (1942), eccentric psychologist Tan Porus explains the behavior of a mysterious species of squid by using imaginary numbers in the equations which describe its psychology. The anthology Imaginary Numbers: An Anthology of Marvelous Mathematical Stories, Diversions, Poems, and Musings (Frucht 2000) includes many other works involving imaginary numbers.

REFERENCES:

Asimov, I. "The Imaginary." Super Science Stories. Nov. 1942. Reprinted in The Early Asimov, Book One. Del Rey, pp. 246-262, 1986.

Brown, D. The Da Vinci Code. New York: Doubleday, 2003.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 211-216, 1996.

Frucht, W. (Ed.). Imaginary Numbers: An Anthology of Marvelous Mathematical Stories, Diversions, Poems, and Musings, 2nd ed. New York: Wiley, 2000.

Mazur, B. Imagining Numbers (Particularly the Square Root of Minus Fifteen). Farrar, Straus and Giroux, 2003.