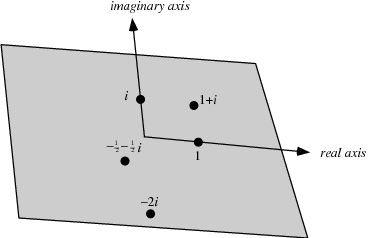
The complex plane is the plane of complex numbers spanned by the vectors 1 and 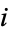, where  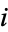is the imaginary number. Every complex number corresponds to a unique point in the complex plane. The line in the plane with  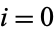is the real line. The complex plane is sometimes called the Argand plane or Gauss plane, and a plot of complex numbers in the plane is sometimes called an Argand diagram.

The complex plane together with the point at infinity {infty}" src="http://mathworld.wolfram.com/images/equations/ComplexPlane/Inline4.gif" style="height:15px; width:49px" /> is known as the Riemann sphere or extended complex plane and denoted 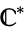 or 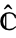. However, the notation  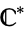is also used to denote the punctured plane {0}" src="http://mathworld.wolfram.com/images/equations/ComplexPlane/Inline8.gif" style="height:15px; width:41px" />.

REFERENCES:

Courant, R. and Robbins, H. "The Geometric Interpretation of Complex Numbers." §5.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 92-97, 1996.

Krantz, S. G. "The Topology of the Complex Plane." §1.1.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 3-5, 1999.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 23, 1986.