Quadratic Integral
المؤلف:
Gradshteyn, I. S. and Ryzhik, I. M
المصدر:
Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
الجزء والصفحة:
...
17-9-2018
2557
Quadratic Integral
To compute an integral of the form
 |
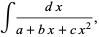(1)
|
complete the square in the denominator to obtain
 |
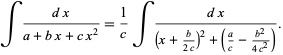(2)
|
Let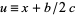 
. Then define
 |
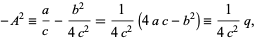(3)
|
where
 |
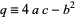(4)
|
is the negative of the polynomial discriminant. If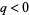 
, then
 |
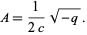(5)
|
Now use partial fraction decomposition,
 |
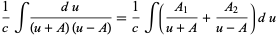(6)
|
 |
(7)
|
so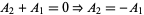 
and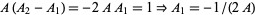 
. Plugging these in,
![1/cint(-1/(2A)1/(u+A)+1/(2A)1/(u-A))du
=1/(2Ac)[-ln(u+A)+ln(u-A)]
=1/(2Ac)ln((u-A)/(u+A))
=1/(2(1/(2c))sqrt(-q)c)ln((x+b/(2c)-1/(2c)sqrt(-q))/(x+b/(2c)+1/(2c)sqrt(-q)))
=1/(sqrt(-q))ln((2cx+b-sqrt(-q))/(2cx+b+sqrt(-q)))](http://mathworld.wolfram.com/images/equations/QuadraticIntegral/NumberedEquation8.gif) |
(8)
|
for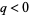 
. Note that this integral is also tabulated in Gradshteyn and Ryzhik (2000, equation 2.172), where it is given with a sign flipped.
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
