


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-9-2017
Date: 14-9-2017
Date: 11-10-2017
|
Died: 25 October 1970 in Alnwick, Northumberland, England
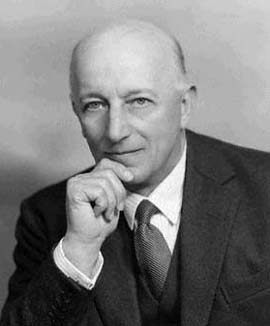
Edward Collingwood's parents were Dorothy Fawcett and Colonel Cuthbert George Collingwood. Colonel Collingwood had a career in the army, commanding the Lancashire Fusiliers in the battle of Omdurman in September 1898. In this battle the Anglo-Egyptian force commanded by Kitchener defeated the Mahdists and established British dominance in Sudan. Colonel Collingwood retired from the army in 1899, the year before his son Edward was born on the family estate of Lilburn Tower. The estate is in Northumberland in the north of England about 7 km from Wooler on the road to Alnwick (which is about 20 km to the south east). Edward was the oldest of his parents four children, all boys, and he was brought up on the family estate enjoying [2]:-
... shooting and fishing and the social life of the country.
We should note that Edward's mother Dorothy came from a well off family, and the name "Foyle" is the name of their family estate. Dorothy [2]:-
... was always a strong influence on the family.
Collingwood was educated at the Royal Naval College Osborne, which he entered in 1913, moving to Dartmouth in the following year. He joined the Navy and became a midshipman in 1915 on the ship HMS Collingwood. This ship was named after Vice-Admiral Cuthbert Collingwood who was Nelson's second in command at the battle of Trafalgar. Vice-Admiral Collingwood was the brother of Edward Collingwood's great-grandfather, and it was no coincidence that Collingwood served on HMS Collingwood for special arrangements had been made for this to happen.
However Collingwood's naval career came to an end when he fell down a hatchway on board ship, broke his wrist and damaged his knee, just before the Battle of Jutland. He was transferred to the hospital ship, then invalided out of the Navy. Attempting to go to Woolwich he failed the medical examination so, in 1918, he entered Trinity College, Cambridge to study mathematics.
Collingwood was influenced by his advisor of studies, Hardy at Cambridge and decided early on that he would undertake research in mathematics. He was also influenced by Littlewood, but his examination performance was relatively poor and he obtained only a Second Class degree in 1922. Although there were many others in Collingwood's year at Cambridge like Burkill, Ingham and Newman, he seems to have had little contact with them. A friend, Gilbert Ashton, writing of these days, wrote that Collingwood was:-
... always known by his friends and contemporaries of Trinity as 'The Admiral' ... I remember The Admiral as a quiet, reserved and rather shy person ...
Cartwright describes how Collingwood behaved as an undergraduate in [2]:-
... he kept somewhat aloof from his mathematical contemporaries, and had a full, but entirely separate, social life among a group, most of whom had served in the forces ... He used his private means to entertain well, but never ostentatiously.
In 1922 Collingwood went to Aberystwyth at the invitation of W H Young. He was awarded the Rayleigh prize from Cambridge in 1923 but failed to obtain a fellowship. It was at this time that he completed his work on generalising Nevanlinna's second fundamental theorem, which became his first paper in 1924. Awarded a Rouse Ball travelling scholarship, he spent 1924-25 at the Sorbonne. Despite his examination results he returned to Cambridge to study for a Ph.D. with Littlewood as his supervisor. He received his doctorate for a thesis entitled Contributions to the theory of integral functions of finite order in 1929. From 1930 he was appointed Steward of Trinity and gave advanced courses on integral and meromorphic functions but gave no undergraduate courses.
In 1937 Collingwood left Cambridge and became High Sheriff of Northumberland. However when World War II began in 1939, he became a naval scientist. As stated in [3]:-
... he got himself into uniform early in the war and his record is impressive.
He was in charge of the Sweeping Division in 1943, then Chief Scientist in the Admiralty Mine Design Department in 1945. For his war work he was awarded the C.B.E. and received the Legion of Merit from the USA in 1946.
After the war he returned to his researches on meromorphic functions, publishing an important paper in 1949. He then undertook research work with Mary Cartwright on the theory of cluster sets. Mary Cartwright writes:-
I tried to contribute what I could to this paper ... my impression is that it was much less than his contribution. I also collaborated in one later paper published in 1961 on an allied topic. ... I found myself quite unable to grasp the deep results in the theory of sets of points on which much of Collingwood's later work in this field depended.
Collingwood became involved with hospital boards in Newcastle, being a founder member of the Newcastle Regional Hospital Board and its chairmen from 1953 to 1968, then later he was involved with medical affairs on a national and international level. He was vice-president of the International Hospital Federation from 1959 to 1967, a member of the medical research council from 1960 to 1968, and he served on the royal commission on medical education from 1965 to 1968. He was chairman of the Council of Durham University for most of the 1950's and 1960's.
He was elected to a fellowship of the Royal Society in 1965. He also served the London Mathematical Society in many ways, as a member of the Council and as Treasurer. He wrote an article in 1951 to mark the centenary of the Society. He was knighted in 1962.
Despite these numerous activities Collingwood still found time for various hobbies. In particular he had a fine collection of eighteenth century paintings, and a collection of Chinese porcelain. As with all his activities Collingwood made a deep study of his hobbies and became a recognised expert on Chinese porcelain.
His character is described in [1]:-
Collingwood was loved and admired both for his achievements and for the delight of his company. ... he had great intellectual powers which enabled him to achieve excellence in diverse activities conducted in parallel and not in series. Born in Glendale in Northumberland he remained a countrymen at heart with practical knowledge of forestry, farming and gardening. ... He remained a bachelor to the grief of the many dancing partners who had been entranced by his waltzing!
His appearance is described in [2]:-
Collingwood was short and fair and walked with long strides. He early became very bald.
Articles:



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
شركة اللواء العالمية تعرض منتجاتها في الأسبوع الزراعي السادس عشر في بغداد
|
|
|