The n₀ and p₀ Equations

We have argued that the Fermi energy for an intrinsic semiconductor is near midgap In deriving the equations for the thermal-equilibrium concentration of electrons n₀ and the thermal-equilibrium concentration of holes p₀. we will not be quite so restrictive. We will see later that, in particular situations, the Fermi energy can deviate from this midgap energy. We will assume initially, however, that the Fermi level remains within the bandgap energy.

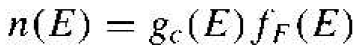(1)

The equation for the thermal-equilibrium concentration of electrons may be found by integrating Equation (1) over the conduction band energy, or

(2)

The lower limit of integration is E_c and the upper limit of integration should be the top of the allowed conduction band energy. However, since the Fermi probability function rapidly approaches zero with increasing energy, we can take the upper limit of integration to be infinity.

We are assuming that the Fermi energy is within the for hidden-energy bandgap For electrons in the conduction hand, we have E > E_c . If (E_c - E_F) >> k T, then (E - E_F) >> kT, so that the Fermi probability function reduces to the Boltzmann approximation, which is

(3)

Applying the Boltzmann approximation to Equation (2), the thermal-equilibrium density of electrons in the conduction band is found from

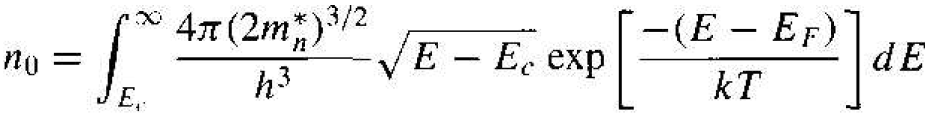(4)

The integral of Equation (4) may be solved more easily by making a change of variable. If we let

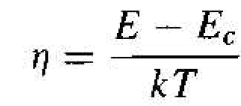(5)

then Equation (4) becomes

(6)

The integral is the gamma function, with a value of

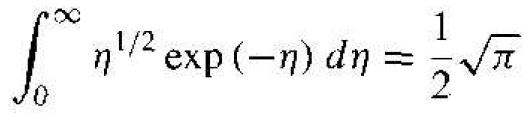(7)

Then Equation (6) becomes

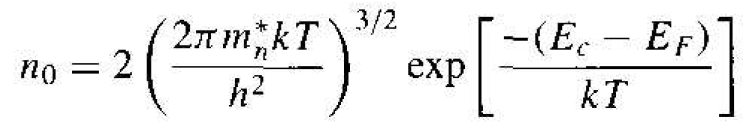(8)

We may define a parameter N_c as

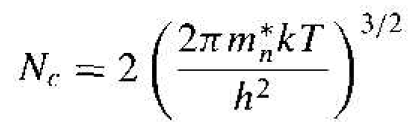(9)

so that the thermal-equilibrium electron concentration in the conduction band can be written as

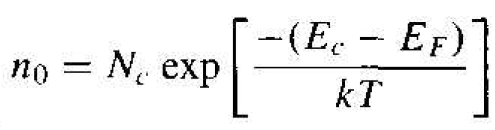(10)

The parameter N_c is called the effective density of states function in the conduction band. If we were to assume that m^*_n = m₀, then the value of the effective density of states function at T = 300 K is N_c = 2.5 × 10^-19 cm^-3, which is the order of magnitude of N_c for most semiconductors. If the effective mass of the electron is larger or smaller than m₀, then the value of the effective density of states function changes accordingly, but is still of the same order of magnitude.

The thermal-equilibrium concentration of holes in the valence band over the valence band energy, or

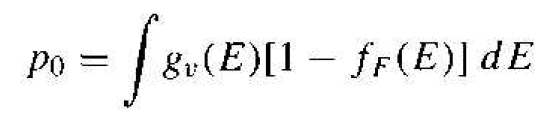(11)

We may note that

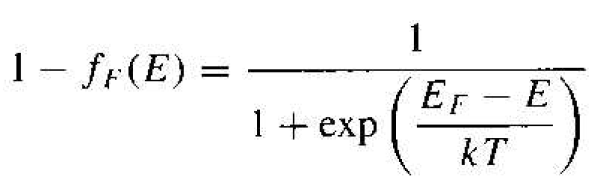(12a)

For energy states in the valence band, E < E_v. If (E_F – E_v) >> kT (the Fermi function is still assumed to be within the bandgap), then we have a slightly different form of the Boltzmann approximation. Equation (12a) may be written as

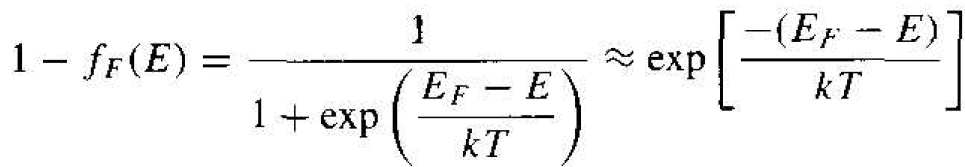(12b)

Applying the Boltzmann approximation of Equation (12b) to Equation (11), we find the thermal-equilibrium concentration of holes in the valence band is

(13)

where the lower limit of integration is taken as minus infinity instead of the bottom of the valence hand. The exponential term decays fast enough so that this approximation is valid.

Equation (13) may be solved more easily by again making a change of variable. If we let

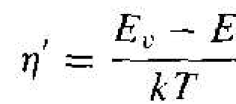(14)

then Equation (13) becomes

(15)

where the negative sign comes from the differential dE = - k T d η' . Note that the lower limit of η' becomes +∞ when E = -∞. If we change the order of integration, we introduce another minus sign. From Equation (7). Equation (15) becomes

(16)

We may define a parameter N_v as

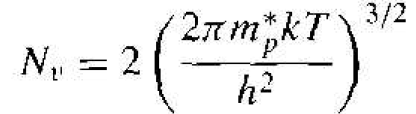(17)

which is called the effective density of states ,function in the valence hand. The thermal-equilibrium concentration of holes in the valence band may now be written as

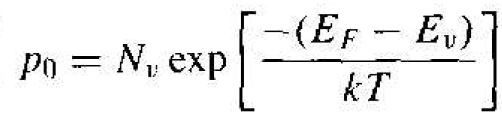(18)

The magnitude of N_v is also on the order of 10¹⁹ cm^-3 at T = 300 K for most semiconductors The effective density of states functions, N_c and N_v, are constant for a given semiconductor material at a fixed temperature. Table 1.1 gives the values of the density of states function and of the effective masses for silicon, gallium arsenide, and germanium. Note that the value of N_c for gallium arsenide is smaller than the typical 10¹⁹ cm^-3 value. This difference is due to the small electron effective mass in gallium arsenide.

The thermal equilibrium concentrations of electrons in the conduction band an of holes in the valence band are directly related to the effective density of states constants and to the Fermi energy level.

Table 1.1 Effective density of states function and effective mass values.