Extension to Semiconductors

In the last section, we derived a general expression for the density of allowed electron quantum states using the model of a free electron with mass m bounded in a three-dimensional infinite potential well. We can extend this same general model to a semiconductor to determine the density of quantum states in the conduction band and the density of quantum states in the valence band. Electrons and holes are confined within the semiconductor crystal so we will again use the basic model of the infinite potential well.

The parabolic relationship between energy and momentum of a free electron as E = p²/2m = h²k²/2m. The conduction energy band in the reduced k space. The E versus k curve near k = 0 at the bottom of the conduction band can be approximated as a parabola, so we may write

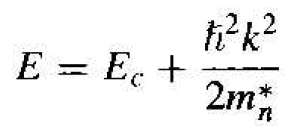(1)

where E_c is the bottom edge of the conduction band and m^*_n is the electron effective mass. Equation (1) may be rewritten to give

(2)

The general form of the E versus k relation for an electron in the bottom of a conduction band is the same as the free electron, except the mass is replaced by the effective mass. We can then think of the electron in the bottom of the conduction band as being a "free'' electron with its own particular mass. The right side of Equation (2) is of the same form a the right, which was used in the derivation of the density of states function. Because of this similarity, which yields the "free" conduction electron model, we may generalize the free electron write the density of allowed electronic energy states in the conduction band us

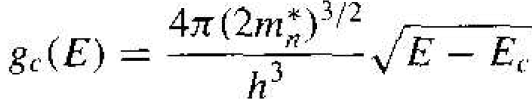(3)

Equation (3) is valid for E ≥ E_c . As the energy of the electron in the conduction band decreases, the number of available quantum states also decreases.

The density of quantum states in the valence hand can be obtained by using the same infinite potential well model, since the hole is also confined in the semiconductor crystal and can be treated as a "free" particle. The effective mass of the hole

is m^*_p. We may also approximate the E versus k curve near k = 0 by a parabola for a "free" hole, so that

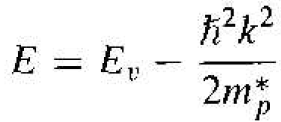(4)

Equation (4) may be rewritten to give

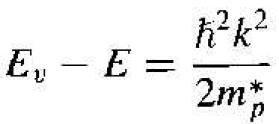(5)

Again, the right side of Equation (5) is of the same form used in the general derivation of the density of states function. We may then generalize the density of states function to apply to the valence band, so that

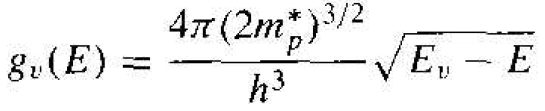(6)

Equation (6) is valid for E ≤ E_v.

We have argued that quantum states do not exist within the forbidden energy band, so g(E) = 0 for E_v < E < E_c. Figure 1.1 shows the plot of the density of quantum states as a function of energy. If the electron and hole effective masses were equal, then the functions g_c(E) and g_v(E) would be symmetrical about the energy midway between E_c and E_v, or the midgap energy. E_midgap.

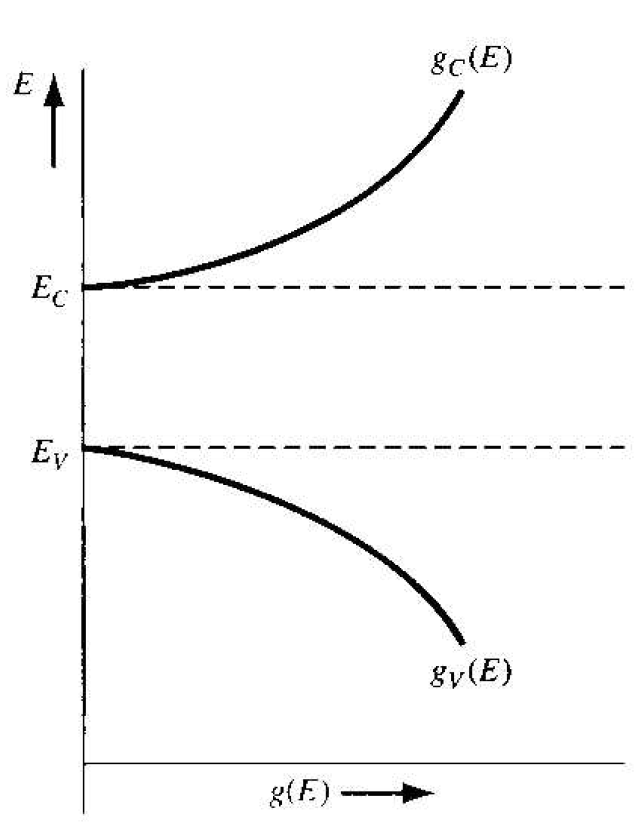
Figure 1.1 The density of energy states in the conduction band and the density of energy states in the valence band as a function of energy.