
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Gravitational field of a rotating black hole
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 138
2-2-2017
1868
Gravitational field of a rotating black hole
1.1 Kerr metric
If a black hole is rotating, the direction of its axis of rotation singles out a preferred direction in space. As a result, spherical symmetry characterizing the spacetime of a non-rotating black hole is broken. The geometry of a rotating black hole is axisymmetric. The Kerr metric describing this geometry written in the coordinates proposed by Boyer and Lindquist [7] is
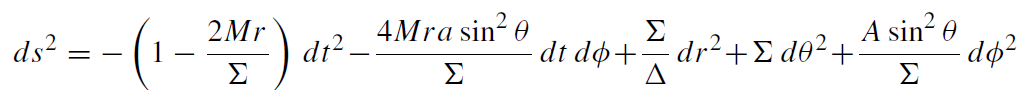 (1.1)
(1.1)
where
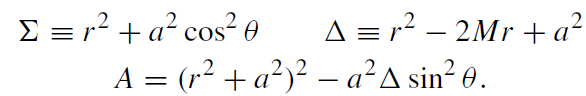 (1.2)
(1.2)
Two constants which enter the Kerr metric are the black hole mass M and the rotation parameter a connected with angular momentum J of the black hole, a = J/M. As for the Schwarzschild metric, one can always rewrite the Kerr metric in the dimensionless form, by extracting the scale parameter of length dimensions from the metric. Since the radius r+ of the event horizon depends on a, it is convenient to use 2M or M as the scaling parameter. The latter option is used more often. Note that in this case the normalization is different from the one used in the Schwarzschild case by an extra factor of two. The only dimensionless parameter which enters the dimensionless form of the Kerr metric is a/M, which can take values in the range (−1, 1). For |a/M| > 1 there is no event horizon and the metric describes a spacetime with a naked singularity.
1.2 Killing vectors
Being stationary (independent of time t) and axisymmetric (independent of an angular coordinate φ) the Kerr metric has two Killing vectors:
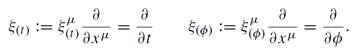 (1.3)
(1.3)
The Kerr geometry and its Killing vectors possess the following properties:
● Since the component gtφ of the metric does not vanish, the Killing vector field ξ(t) is tilted with respect to the section t = constant. The tilting angle depends on r and θ.
● The infinite redshift surface where ξ2(t)≡ gt t = 0 does not coincide with a Killing horizon. This surface where
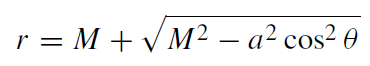 (1.4)
(1.4)
is an external boundary of the ergosphere.
● The event horizon lies at Δ = 0, that is at r = r+, where
 (1.5)
(1.5)
● The event horizon again coincides with the Killing horizon determined by the equation
η2 = 0 (1.6)
where ημ = ξμ(t)+ ΩHξμ(φ), and
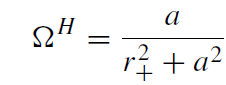 (1.7)
(1.7)
is the angular velocity of the black hole.
● The infinite redshift surface lies everywhere outside the event horizon except at the two poles θ = 0 and θ = π. Inside the ergosphere, that is, between the infinite redshift surface and the horizon, the Killing vector field ξ(t) is spacelike, ξ2(t) > 0.
1.3 Killing tensor
The dragging effect connected with the rotation of the black hole affects orbits of test particles. As a result, only orbits lying in the equatorial plane are planar. Two integrals of motion connected with two Killing vectors together with the proper time normalization condition are sufficient to reduce the equation of motion to a complete set of first integrals. To proceed with non-equatorial orbits an additional integral of motion is required. Fortunately such an integral exists for the Kerr geometry. It is connected with a Killing tensor.
A Killing tensor is a symmetric tensor field ξμν obeying the equation
ξ(μν;λ) = 0. (1.8)
In the same manner as for the Killing vector, one can show that for a geodesic motion the quantity
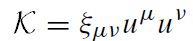 (1.9)
(1.9)
remains constant along the worldline. Indeed
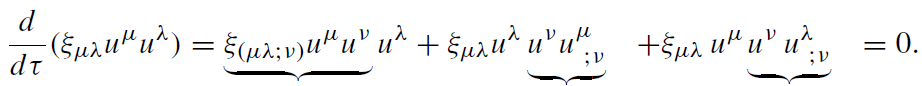 (1.10)
(1.10)
It is easy to check that a tensor product ξ(1) μ ξ(2) ν of two Killing vectors ξ(1) μ and ξ(2) ν is a Killing tensor. In this case the corresponding conserved quantity is a product of two integrals of motion of the Killing vectors. A nontrivial conservation law is connected only with a Killing tensor which is linearly independent of tensor products of the Killing vectors. For the Kerr metric, such an independent Killing tensor has the following non-vanishing components in the Boyer–Lindquist coordinates
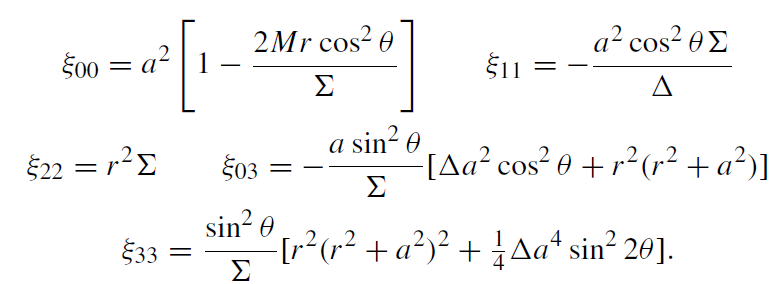 (1.11)
(1.11)
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















