1.1 Killing vectors

A Killing vector field ξ^μ is a vector field which satisfies the Killing equation

 ξ(μ;ν) = 0. (1.1)

A Killing vector is a generator of a symmetry transformation on a spacetime manifold. Killing trajectories are integral lines of the Killing vector field,

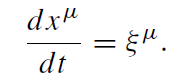 (1.2)

If ξ^μ is regular, Killing trajectories form a foliation and one can introduce (at least locally) coordinates (t, yⁱ ) where t is a parameter along the trajectory, and the yⁱ are constant on a given trajectory. It is easy to show that the metric g_μν in these coordinates does not depend on t. This demonstrates explicitly the symmetry of the spacetime carrying a Killing vector.

1.2 Integrals of motion

For a geodesic motion the quantity ξ_μ u^μ is constant along the particle world line and hence it is an integral of motion. This follows from

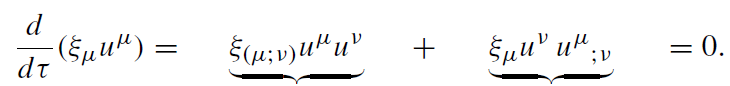 (1.3)

1.3 Symmetries of Schwarzschild spacetime

Being static and spherically symmetric, the Schwarzschild metric has four linearly independent Killing vector fields. One of them, in Schwarzschild coordinates,

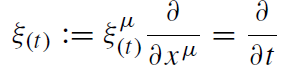 (1.4)

is connected with the time symmetry. The other three are generators of the three parameter group of rotations preserving the geometry on a unit sphere:

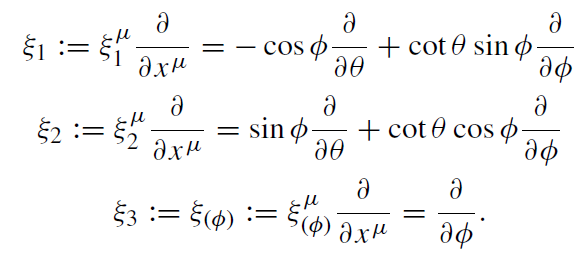 (1.5)

The latter vector generates rotation around a z-axis passing through the north θ = 0 and south θ = π poles of the black hole.

The Killing vector ξ(t ) possesses the following properties:

● ξ(t ) is orthogonal to the surface t = constant. This property follows from the invariance of the metric with respect to time reflection t → -t. (The metric is not only stationary but also static.)

● The infinite redshift surface where ξ²_(t) = g_{t t} = 0 coincides with a Killing horizon, which in its turn coincides with the event horizon, see later.