1.1 Equations of motion

When the energy E is much larger than m, a particle is called ultrarelativistic. In this limit Ẽ → ∞ and ˜L → ∞while the ratio ˜L /Ẽ remains finite and is equal to  ˜b := b/r_S, where b is the impact parameter of the particle at infinity. The equations of motion of the ultrarelativistic particle (or a light ray) take the form (˜t = t/r_S):

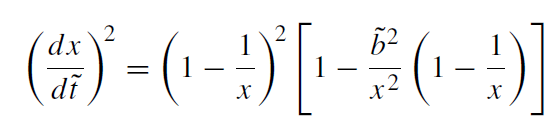 (1.1)

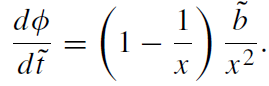 (1.2)

The sign of b depends on the sense of motion; we assume that b is positive. The radial turning point on the trajectory is defined by the equation

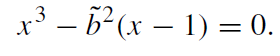 (1.3)

The impact parameter b as a function of the position of a radial turning point is shown in figure 1.1.

1.2 Types of trajectory

In figure 1.1, the motion of an ultrarelativistic particle with a given b is represented by a horizontal line b = constant. A particle approaches the black hole,

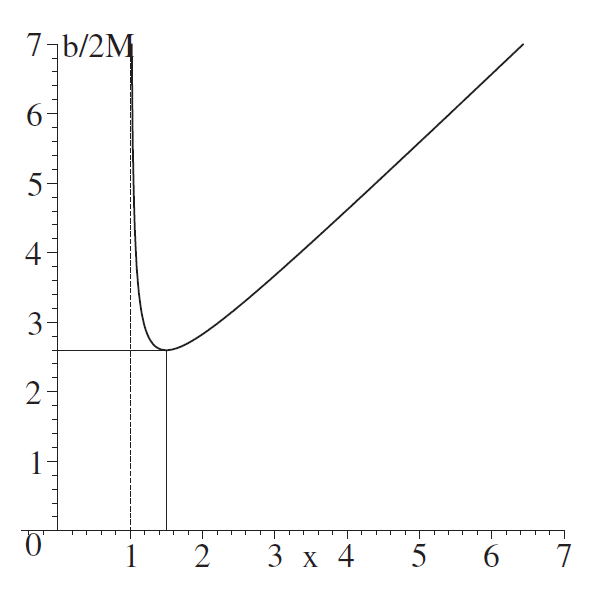
Figure 1.1. Impact parameter b as a function of the position of extrema in x = r/r_S on the trajectory of an ultrarelativistic particle.

passes by it at the minimal distance corresponding to the point of intersection of b = constant with the right-hand branch of the b(r ) curve, and again recedes to infinity. If the intersection occurs close to the minimum b_min = 3√3 × r_S/2, the particle may experience a number of turns before it flies away to infinity. The  exact minimum of the curve b(r) corresponds to the (unstable) motion on a circle of radius  r = 1.5r_S at the velocity v = c. Note that the left-hand branch of b(r) in figure 1.1 corresponds to the maximum distance between the ultrarelativistic particle and the black hole; the particle first recedes to r < 1.5r_S but then again falls into the black hole. Obviously, for such a motion the parameter b does not have the literal meaning of the impact parameter at infinity since the particle never recedes to infinity. For a given coordinate r , this parameter can be found as a function of the angle ψ between the trajectory of the particle and the direction to the center of the black hole:

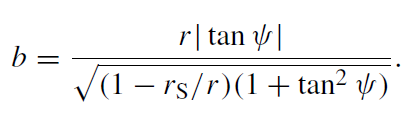 (1.4)

If an ultrarelativistic particle approaches the black hole on the way from infinity and the parameter b is less than the critical value bmin = 3√3r_S/2, the particle falls into the black hole.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر