1.1 Orbits are planar

Consider a particle moving in the Schwarzschild metric. Using spherical symmetry, one can always choose coordinates so that at the initial moment τ₀ one has θ₀ = π/2 and (dθ/dτ)|₀ = 0. Since the only non-vanishing components of Γ^θ_μν are

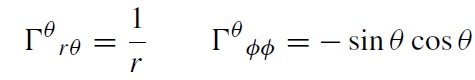 (1.1)

the θ-component of the geodesic equation of motion takes the form

 (1.2)

A solution of this equation for the given initial data is θ = π/2. Thus, the trajectory of a particle is planar and we can assume it to lie in the equatorial plane θ = π/2.

1.2 Effective potential

The Schwarzschild metric is invariant under time t and angular coordinate φ translations. The corresponding conserved quantities are (θ = π/2):

 (1.3)

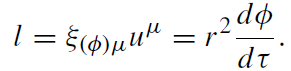 (1.4)

Ẽ = E/m is the specific energy of a particle (E being the energy, and m being the mass of the particle). The quantity l = L/m is the specific angular momentum of a particle (L being its angular momentum). For the motion in the equatorial plane, the total angular momentum coincides with the azimuthal angular momentum. For a motion of the particle in the black hole exterior, both t and φ are monotonic functions of τ .

Using these relations and the normalization condition for the four-velocity u^μ

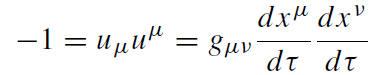 (1.5)

one gets :

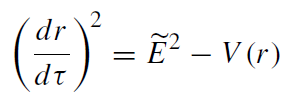 (1.6)

where we introduced the effective potential

 (1.7)

Figure 1.1. Effective potential U(x) as a function of x = r/r_S and for a specific angular momentum ˜L of a particle.

1.3 Properties of the effective potential

Different types of particle trajectory can be classified by studying the turning points of its radial motion where

V (r ) = Ẽ².    (1.8)

The only scale parameter in the problem is the gravitational radius of the black hole. Using again the dimensionless coordinate x and ˜L = l/r_S we can rewrite V (x) according to

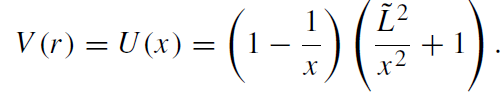 (1.9)

The effective potential U(x) is shown in figure 1.1. For fixed |˜L | ≥ √3, U as a function of x has a maximum at x₊ and a minumum at x₋, where

 (1.10)

For ˜L = √3, x₋ = x₊ = 3. A heavy full line in figure 5.1 shows the position of the extrema.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر