Unfortunately, the scenario described in the preceding section cannot be extended without difficulty to matter with angular momentum. Though we do not possess a dynamical model for collapsing matter, we expect some insight into the process of the formation of rotating black holes by the discussion of an ‘adiabatic’ transition. For this purpose, we consider a stationary and axisymmetric global solution to Einstein's equations describing a rigidly (uniformly) rotating disk of dust. The solution allows a ‘parametric’ collapse, i.e. it has a black hole limit for characteristic values of its parameters. In the following we present some details of the solution which has been found by Neugebauer and Meinel [20] as the solution of a boundary value problem first formulated and approximately solved by Bardeen and Wagoner [21, 22].

The line element of any stationary and axially symmetric solution for isolated and uniformly rotating sources can be cast into the form

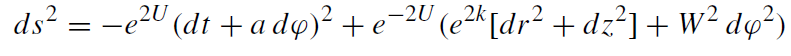 (1.1)

where r, z, ϕ are cylindrical coordinates. The Newtonian gravitational potential U, the gravitomagnetic potential a, the superpotential k, and the aximuthal

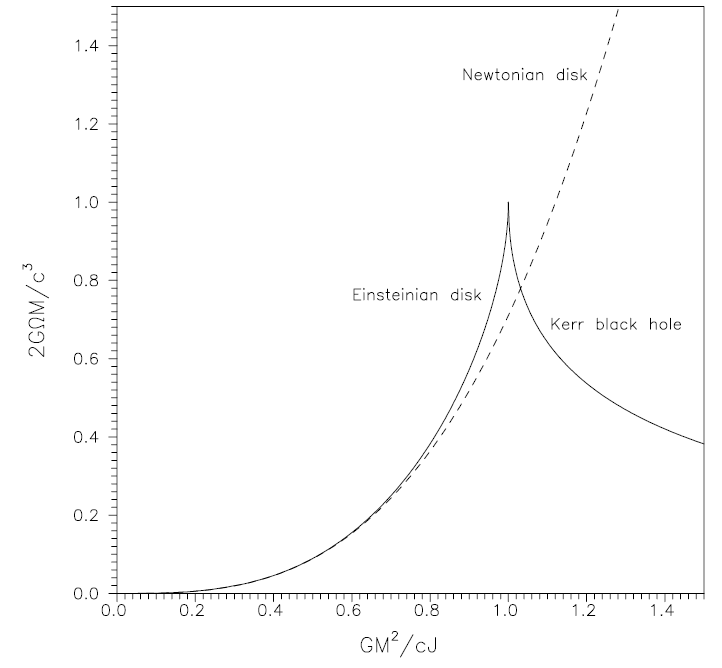
Figure 1.1. Relation between ΩM and M²/J for the Newtonian Maclaurin disk (broken curve), the general-relativistic dust disk and the Kerr black hole. The plot illustrates the phase transition from the disk to the black hole at M2 = J .

potential W depend on r and z alone, i.e. the metric (1.1) allows an Abelian group of motions G2 with the generators (Killing vectors) ξⁱ, ηⁱ ,

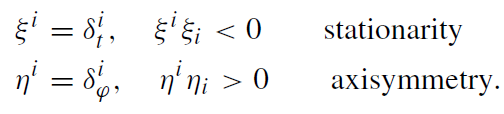 (1.2)

Outside matter, one may choose W = r . Rotational motion of the matter about the symmetry axis z means

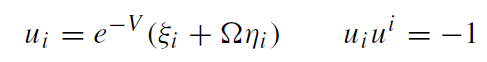 (1.3)

i.e. the four-velocity ui is a linear combination of the Killing vectors. For rigidly rotating bodies, such as our disk of dust, the angular velocity is a constant

Ω = constant.   (1.4)

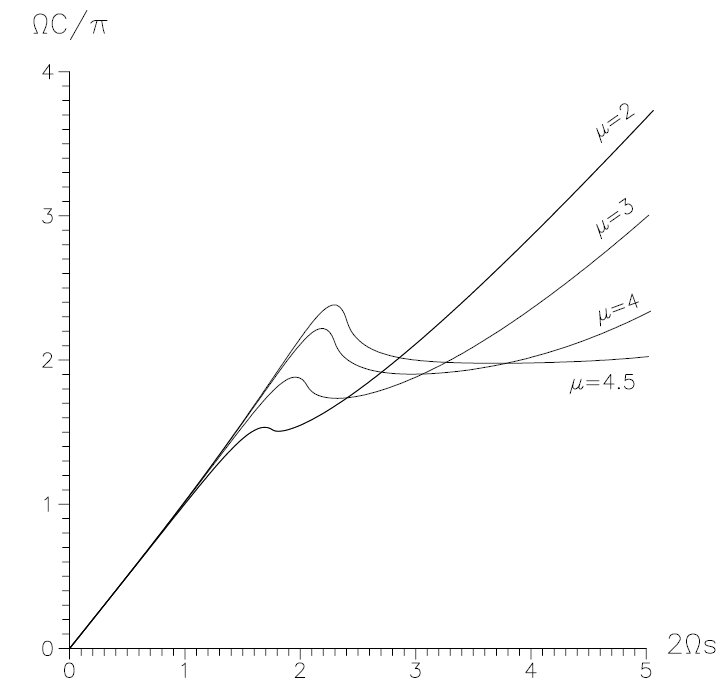
Figure 1.2. Geometry in the disk plane. The circumferential diameter C/π of a circle around the centre of the disk versus the real distances from the centre for increasing values of μ (here ΩC/π and Ωs are dimensionless quantities, c = 1) are depicted.

The task of solving the Einstein equations with the energy–momentum for an infinitesimally thin rigidly rotating disk of dust leads to the following boundary value problem: find a regular solution of Einstein's vacuum equations in the form (1.1), where

(i) the line element (1.1) becomes Minkowskian at infinity,

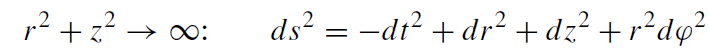 (1.5)

and

(ii) the co-rotating potentials U' = V and a', as measured by an observer comoving with the disk, satisfy the conditions

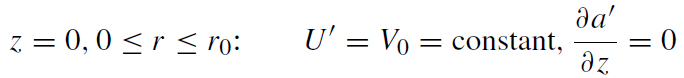 (1.6)

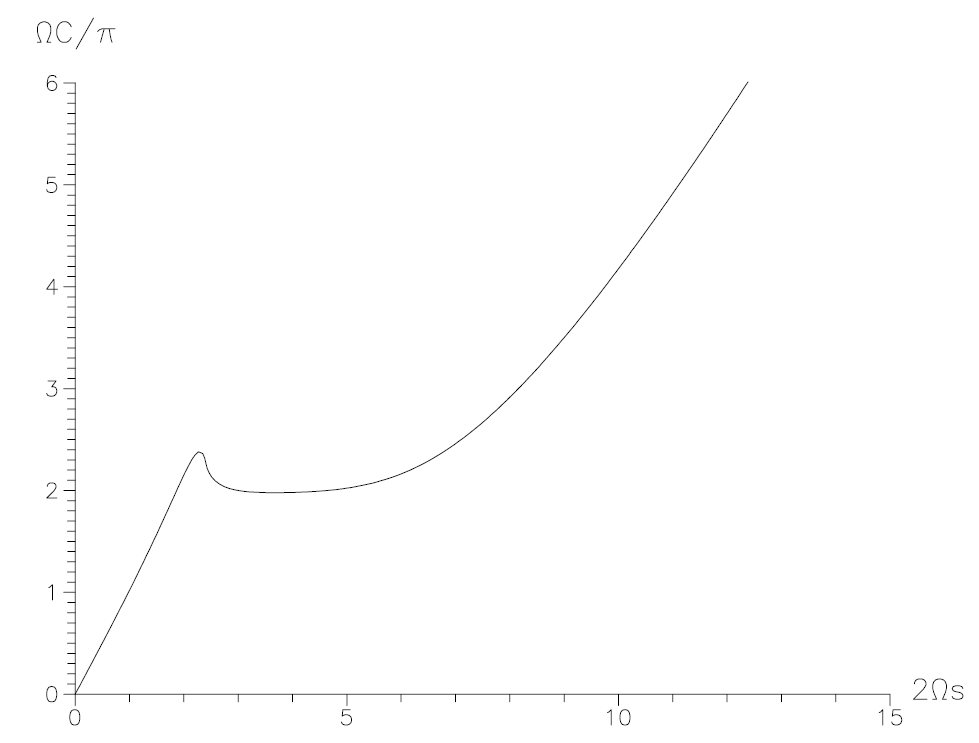
Figure 1.3. For ultrarelativistic values of μ (here μ = 4.5), the ‘interior region’ around the disk (around the local maximum on the left-hand side) is far from the ‘exterior region’ (right-hand ascending branch of the curve), which becomes more and more Kerr-like.

in the disk (r₀ is the coordinate radius of the disk). Equations (1.3) and (1.2) imply

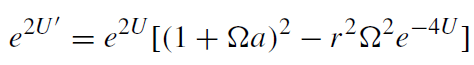 (1.7)

which means that the boundary conditions contain two constant parameters, V₀ and Ω. Consequently, the disk of dust solution is a two-parameter solution. Unfortunately, there is not enough space (or time) to write out the solution explicitly and to prove the facts on which the following description is based. Readers are referred to the original papers [20–23].

An impression of the ‘parametric’ collapse of the disk can be gained from the parameter relations

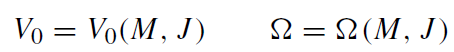 (1.8)

which connect the disk parameters V₀ and Ω with the far-field parameters (energy mass) M and angular momentum J [23]. Figure 1.1 combines the parameter relations between ΩM and M²/J for the classical Maclaurin disk (broken curve), the general-relativistic disk, and the Kerr black hole. It indicates a phase transition from the disk to the extreme Kerr black hole at M²/J = 1 and 2ΩM = 1. This

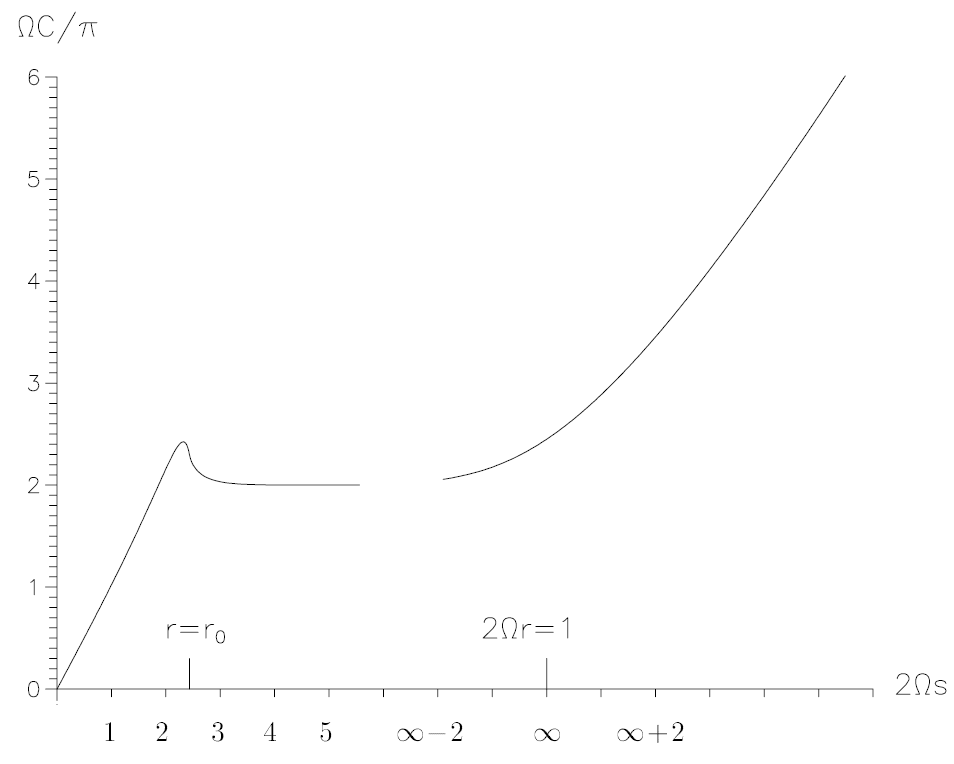
Figure 1.4. In the limit μ = μ₀, the ‘disk world’ (left-hand branch) and the ‘world of the extreme Kerr black hole’ (right-hand branch) are separated from each other. The point labelled ∞ on the abscissa corresponds to a coordinate radius  r = 1/2Ω. Points of the ‘Kerr world’ (right-hand branch) are at infinite distance from the disk (in the left-hand branch).

behaviour of rotating matter is completely different from that of static spherically symmetric fluid spheres which have to obey the restriction R > (9/4)(GM/c²) (R, radius; M, mass of the sphere) and cannot therefore occupy the infinitesimal neighbourhood (2GM/c2 ≤ R ≤ (9/4)(GM/c2)) of their black hole state at R = 2(GM/c²). Figures 1.2-1.4, which correspond to the original, convey a more detailed picture of the parametric black hole transition (‘collapse’) of the disk. They show the circumference C of a circle in the disk plane about the centre of the disk versus the real distance s from the centre,

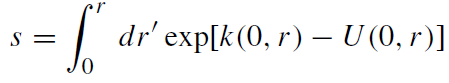 (1.9)

for different values of the parameter μ,

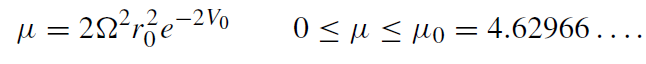
The limits μ → 0 and μ → μ₀ mark the non-relativistic Maclaurin disk and the ultra-relativistic limit, respectively. For increasing values of μ, figures 1.2-1.4 illustrate a separation process for two domains of the disk solution which results, as indicated in figure 1.4, in a disk world (left-hand branch, limit 1) at an infinite distance from the world of an extreme (M² = J ) Kerr black hole (right-hand branch, limit 2). A detailed analysis of the complete solution confirms the result: for μ → μ₀, there are two limits of the disk spacetime. Whether or not this phenomenon can also be found for a dynamical collapse must remain the fruit of future work.

اخر الاخبار

اخبار العتبة العباسية المقدسة

أهالي كربلاء يحيون اليوم السابع لذكرى شهادة الإمام الحسين (عليه السلام)

مشروع أمير القراء الوطني يشهد مشاركة أكثر من 100 طالبٍ في مرحلته الثالثة

قسم الشؤون الفكرية يصدر دليلًا يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة

قسم الشؤون الفكرية يعلن عن توفير عددٍ من المكتبات الإلكترونية المتخصّصة للمؤسّسات الدينية والمكتبات العامّة

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر