
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Relaxation oscillations
المؤلف:
H. HAKEN
المصدر:
LASER LIGHT DYNAMICS
الجزء والصفحة:
vol 2 ، p67
26-12-2016
2118
Relaxation oscillations
In this section we wish to further study the time dependent processes in the single mode laser. But we shall no more assume that the inversion follows the photon number instantaneously. While this assumption is well justified if the photon numbers are small this is no more the case for higher photon numbers. Instead we consider small deviations of n and the occupation numbers from their corresponding stationary values. To this end we assume that n or N, initially deviate from their stationary states a little. We wish to show that n and Nj perform damped oscillations or, in other words, relaxation oscillations. Let us consider as an example a 3-level laser in which the optical transition occurs between the two upper levels. The corresponding occupation numbers are again denoted by N1 and N2. Let us assume that the lower transition from level 1 to level 0 takes place very rapidly (compare also the exercise at the end of this section). In this case the laser equations read as follows: Equation for the photons
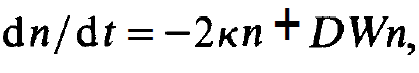 (1.1)
(1.1)
where D= N2- N1.
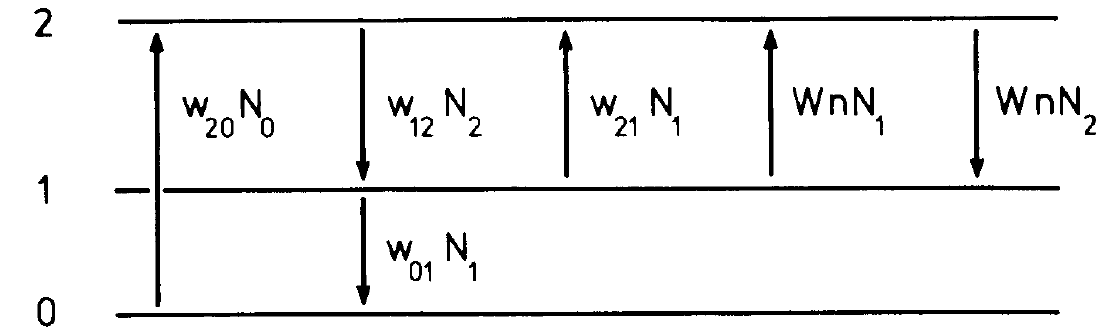
Fig. 1.1. Transition scheme in a system of three-level atoms in which the optical transition takes place from the uppermost to the middle level.
Equation for the occupation numbers
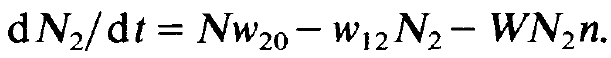 (1.2)
(1.2)
N is the total number of atoms. Because of our assumption that the lower laser level is practically unoccupied we may replace D by N2 in the equation for the photons. We now assume that deviations of n and N2 from their stationary states N0 and N02, respectively, have occurred. We study whether and in which way a stationary state will be reached again. To this end we make the hypothesis
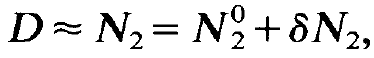 (1.3)
(1.3)
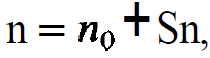 (1.4)
(1.4)
where the stationary solutions n0 and N02 are fixed by the conditions
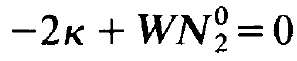 (1.5)
(1.5)
and
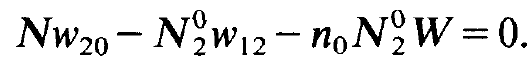 (1.6)
(1.6)
Inserting (1.3) and (1.4) in (1.1) and (1.2) we obtain terms which contain only the stationary solution, terms proportional to δn or δN2 and finally expressions which contain the product Sn δN2. We assume that the deviations from the equilibrium values are only small. This allows us to neglect the term Sn δN2 being of higher order. Because the stationary solution obeys the eqs. (1.5) and (1.6), this solution drops out and we only retain the equations
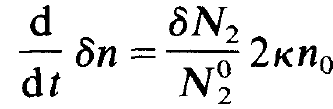 (1.7)
(1.7)
and
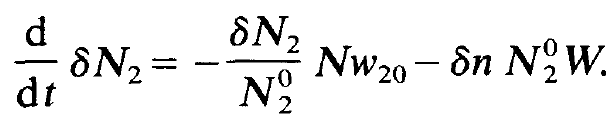 (1.8)
(1.8)
These are two coupled linear differential equations which we can solve as usual by the exponential ansatz
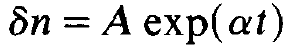 (1.9)
(1.9)
and
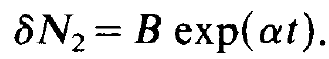 (1.10)
(1.10)
We insert (1.9) and (1.10) in (1.7) and (1.8), perform the differentiation with respect to time, and divide the resulting equations by the exponential function. We then obtain the following two equations
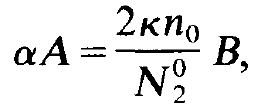 (1.11)
(1.11)
and
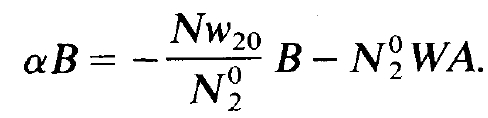 (1.12)
(1.12)
These are homogeneous equations for the unknowns A and B. According to elementary theorems of algebra a non-trivial solution is possible only if the corresponding determinant
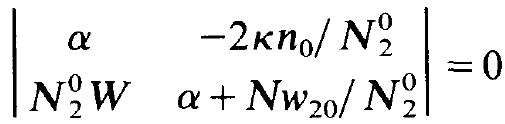 (1.13)
(1.13)
vanishes. This determinant can be easily evaluated. Inserting the values for N02 and n0 according to (1.5) and (1.6) we obtain an equation for a:
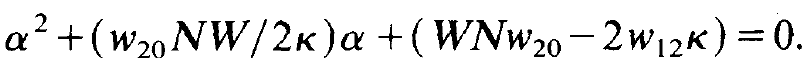 (1.14)
(1.14)
We represent the solution of this quadratic equation in the form
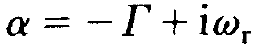 (1.15)
(1.15)
where Γ is given by
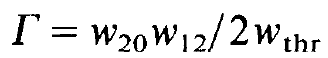 (1.16)
(1.16)
and wr by
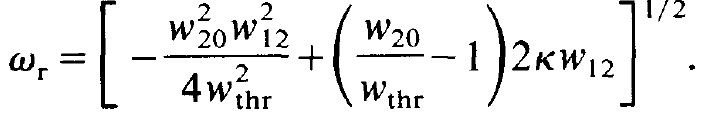 (1.17)
(1.17)
We have assumed that the second term in the bracket in (1.17) is bigger than the first term, so that wr is a real frequency. Furthermore we have used the abbreviation
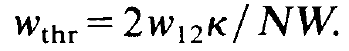 (1.18)
(1.18)
The index "thr" is an abbreviation of "threshold". The most general solution for the photon number may be represented in the form
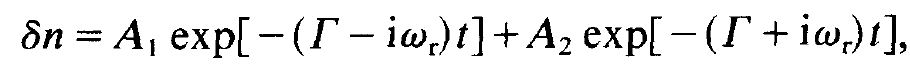 (1.19)
(1.19)
where A1 and A2 are fixed by the initial conditions for the photon number n and the occupation number N2. Obviously the system relaxes towards the stationary state while it performs oscillations (fig. 1.2).
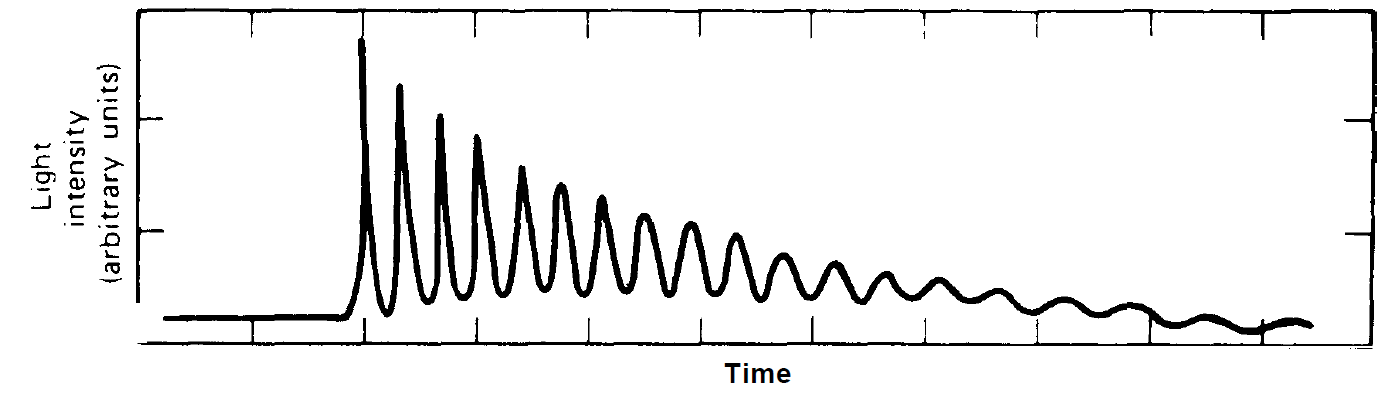
Fig. 1.2. Example of relaxation oscillations.
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















