
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Dimensionless quantities for the light field, and introduction of a coupling constant
المؤلف:
H. HAKEN
المصدر:
LASER LIGHT DYNAMICS
الجزء والصفحة:
vol 2 ، p118
22-12-2016
2280
Dimensionless quantities for the light field, and introduction of a coupling constant
In the following we shall introduce dimensionless variables bλ and bλ* instead of the mode amplitudes Eλ(+) and Eλ(-) respectively. The quantities Eλ and bλ differ by a simple factor only, namely
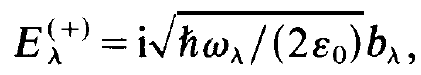 (1.1)
(1.1)
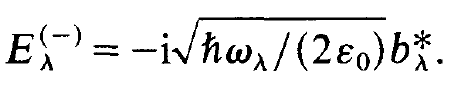 (1.2)
(1.2)
As one may show, the energy of an electric field with mode amplitude Eλ is proportional to |Eλ|2. On the other hand, in a quantum theoretical treatment h⍵λ is just the energy of a photon. Since bλ is dimensionless we recognize that |bλ|2 must have the meaning of a photon number, may be except for a numerical factor. As it will turn out later, |bλ|2 is precisely the average photon number. We shall elucidate this relation in a later chapter when dealing with the laser equations quantum theoretically. We then recognize that there always the combination ϑ21 uλ (xμ)occur s (or the conjugate complex quantity). Furthermore the factor 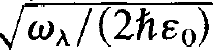 occurs. In order to save space it suggests itself to replace this combination by a quantity which we define by
occurs. In order to save space it suggests itself to replace this combination by a quantity which we define by
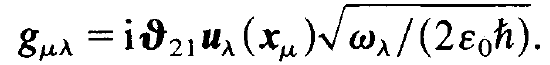 (1.3)
(1.3)
It is a rather simple but boring task to rewrite the laser equations by means of the new quantities just introduced. Therefore we shall write down the laser equations in the next section without any intermediate steps
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















