The laser condition

Let us consider the laser depicted more closely, and let us discuss the tasks of its individual parts. The two mirrors mounted at the endfaces fulfil the following functions. When we treat light as a wave, between the two mirrors only standing waves can be formed. Their wave-lengths, A, are connected with the distance between the mirrors, L, by the relation n λ / 2 = L where n is an integer. We shall briefly discuss the influence of the finite size of mirrors on the formation of these standing waves. On the other hand, when we consider light as consisting of photons, the two mirrors reflect photons running in axial direction again and again. Therefore these photons can stay relatively long in the laser, whereas photons which run in other directions leave the laser quickly. Thus the mirrors serve for a selection of photons with respect to their lifetimes in the laser.

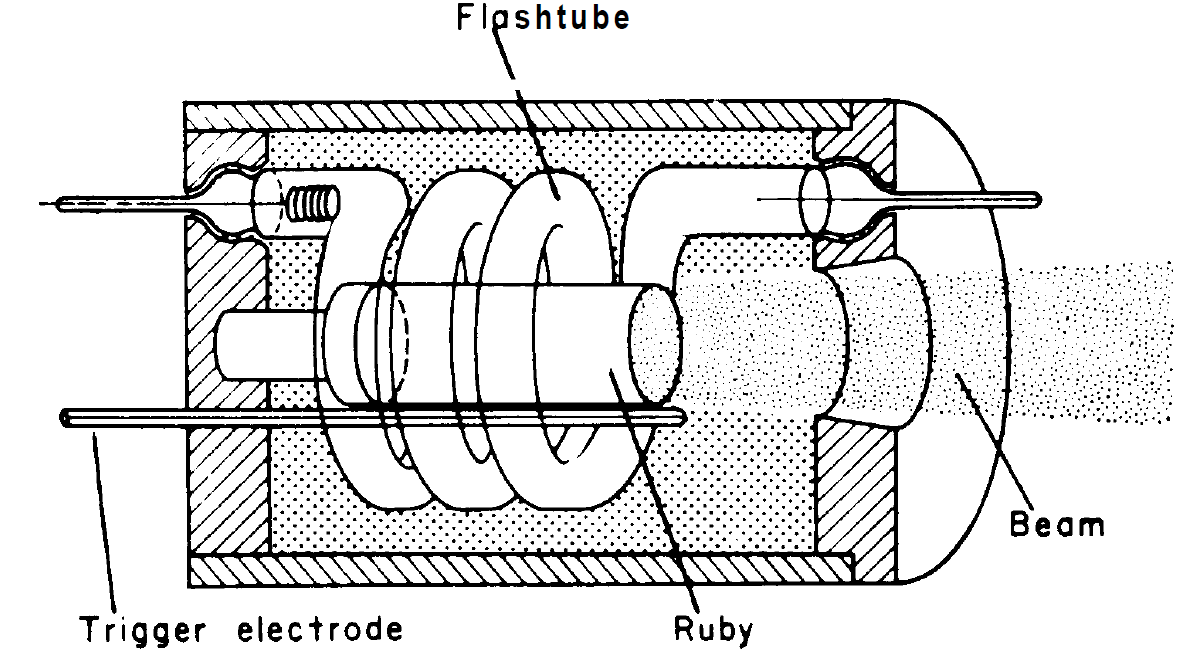
Fig. 1.1. The first experimental set-up of the ruby laser according to Maiman. The ruby rod in the middle is surrounded by a flash lamp in form of a spiral.

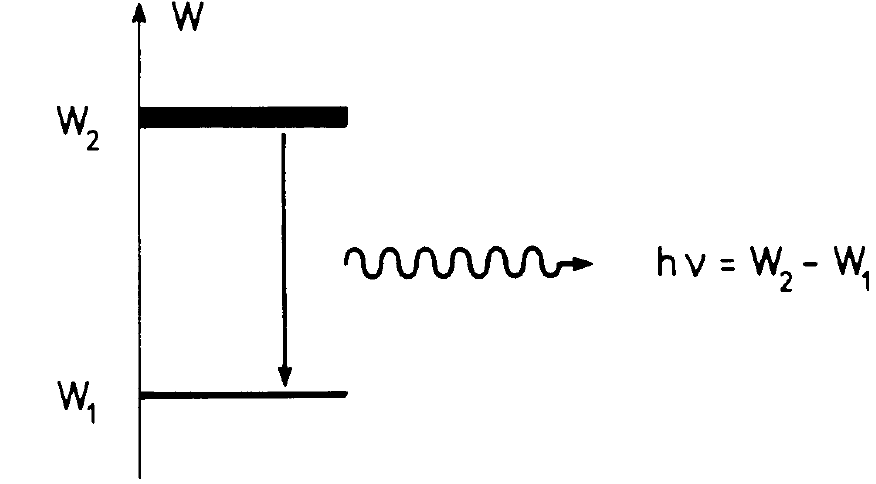
Fig. 1.2. The energy W of a two-level atom with the energy levels W, and W, of which the upper one is occupied. During the transition from level 2 to level 1 a photon of quantum energy hv = W₂ - W, is emitted.

Let us consider a single kind of photons, for instance those which run in axial direction and which belong to a certain wave-length A, and let us study how their number n changes on account of the processes within the laser. To this end we have to make some assumptions on the atoms participating in laser action. We assume that each of the laser atoms has two energy levels between which the optical transition which leads to laser action takes place (fig. 1.2). The external pump light serves the purpose to bring a sufficiently large number of atoms into the excited states of the atoms, whose number we denote by N₂. The rest of the atoms with number N₁ remains in the ground state (fig. 1.3). The excited atoms emit photons spontaneously with a rate proportional to the number of excited atoms, N₂. Denoting the rate with which a single excited atom generates a photon per second by W, the total spontaneous emission rate of photons reads WN₂. As we know, in addition photons can be generated by stimulated emission. The corresponding generation rate can be simply obtained from the spontaneous emission rate by a multiplication by n, i.e. for stimulated emission the generation rate is N₂ Wn. On the other hand, atoms in their ground states, absorb photons with the absorption rate – N₁ Wn. Finally we must take into account that the photons may leave the laser, for instance by passing through one of the mirrors or by scattering by impurities in the laser, etc. We denote the inverse of the corresponding lifetime, t₁, of the photons by 2 k. he loss rate is then given by - 2 k n .Adding up the contributions which stem from the individual processes just mentioned we obtain the fundamental laser equation

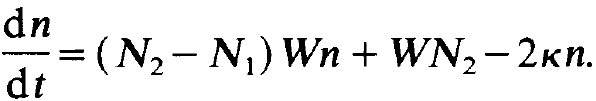     (1.1)

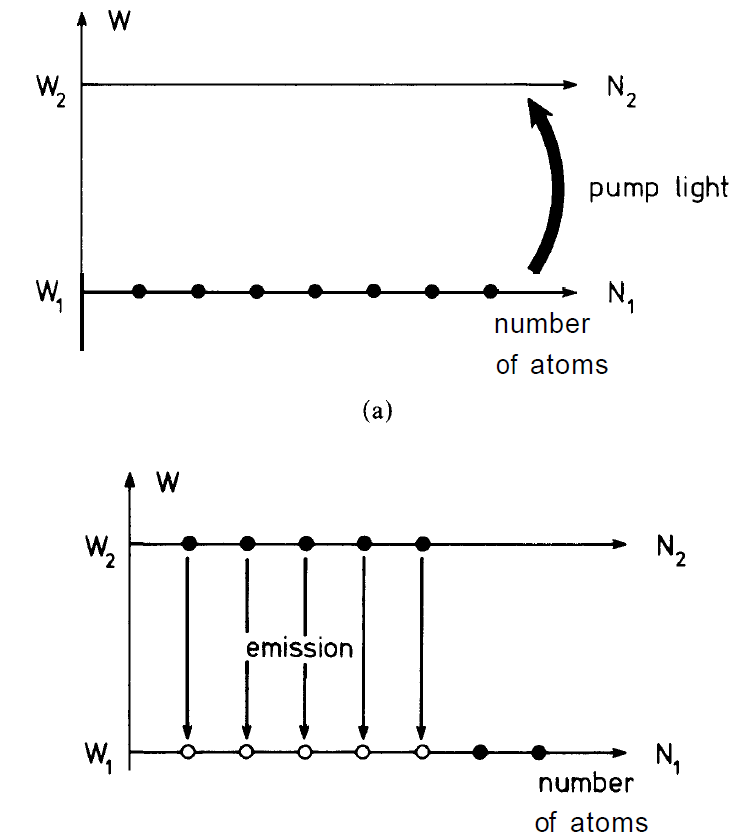
Fig. 1.3. (a) Through the pump mechanism a number of atoms are lifted from their levels 1 into their levels 2. Thus the number of atoms in their ground states, N,, is lowered and those of the atoms in their excited states increased. (b) The excited atoms can make transitions into their ground states by light emission.

The explicit expression for W was derived. Let us rederive that result by some plausibility arguments. The spontaneous emission rate of an atom with respect to all possible kinds of photons is connected with the lifetime τ of the atom with respect to spontaneous emission by W = 1/τ. In the present context we are interested in the transition of the atoms leading to spontaneous emission of a specific kind of photons only. Therefore we have to divide the transition rate per second, 1/τ, by the number of all kinds of photons possible. Therefore we have to form W = l / ( τ p ) ,w here according to the number p is given by

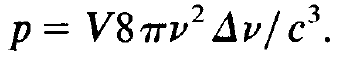    (1.2)

In it V is the volume of the laser, v the laser light frequency, Δv the atomic line-width and c the velocity of light in the laser medium. By means of the formulas derived above we may immediately present the laser condition. Laser action sets in if n increases exponentially. This is guaranteed if the r.h.s. of eq. (2.1) is positive, where we have neglected the spontaneous emission rate WN₂ which is then negligible. In a detailed quantum theoretical treatment  we shall see that in addition to the argument just presented the light spontaneously emitted (which is described by the term WN₂) is incoherent whereas stimulated emission gives rise to coherent light. Using the abbreviations for W and K we immediately obtain the laser condition

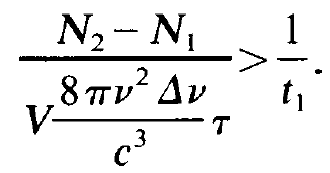    (1.3)

This condition tells us which laser materials we have to use and how we have to construct a laser. First of all we have to take care that the lifetime t₂  of photons within the laser is big enough. As we shall see below this can be reached by making the distance between the mirrors sufficiently large. In order to find an estimate of t₁ we imagine that the photons run in axial direction and that they quit the laser with a certain probability each time they hit one of the mirrors. This probability can be expressed in a simple way by the reflectivity, R, of the mirrors. As one readily sees, the lifetime of a photon is proportional to the distance between the mirrors, inversely proportional to the velocity of light, and inversely proportional to 1 - R. We thus obtain the relation

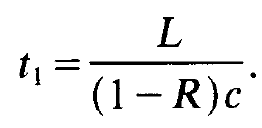  (1.4)

In order to treat a concrete example let us put

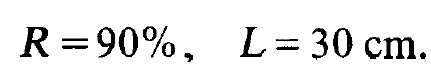 (1.5)

We thus obtain

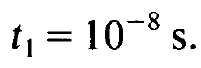   (1.6)

Now let us discuss the left hand side of the inequality (1.3). In order to fulfil (1.3) we must make N₂ - N,, i.e. the inversion, as big as possible. The volume V should be as small as possible or, if we form the ratio between the inversion and the volume, the inversion per volume or, in other words, the inversion density, must be sufficiently large. The factor u² should be as small as possible but because in each case one wants to generate light of a specific wave-length the size of v² is fixed and cannot be circumvented. But we see that with increasing frequency it becomes increasingly more difficult to fulfil the laser condition which makes it so difficult to build an X-ray laser. Both the atomic line-width Av and the lifetime τ of an atom (with respect to light emission) should be chosen as small as possible. But here fundamental limits exist. As is known from quantum mechanics, the uncertainty relation Δvτ ≥ 1 holds. Inserting some typical data such as

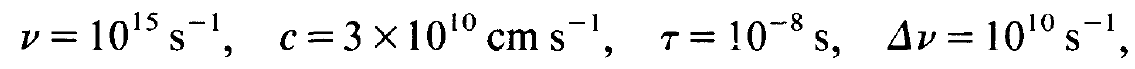  (2.7)

we obtain the inversion density which is necessary for laser action

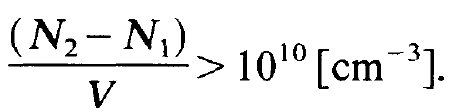     (1.8)

We shall get to know a number of pump mechanisms by means of which we may achieve the necessary inversion.