The problems of laser theory

In this book we shall focus our attention on the theoretical treatment of the laser process. As we shall see, a wealth of highly interesting processes are going on in the laser and we shall treat them in detail. But what are the physically interesting aspects and problems of a laser theory? To this end we have to realize that within a laser very many laser-active atoms, say l0¹⁴ or more, are present which interact with many laser modes. Thus we have to deal with a many-particle problem. Furthermore the laser is an open system. On the one hand the laser emits all the time light through one of its mirrors which has some transmissivity, and on the other hand energy must be continuously pumped into the laser in order to maintain the laser process. Thus the system is open with respect to an energy exchange with its surrounding. Because the atoms are continuously excited and emit light, the atomic system is kept far from thermal equilibrium. Over the past years it has become evident that the laser represents a prototype of systems which are open and far from thermal equilibrium. Clearly the optical transitions between the atomic levels must be treated according to quantum theory. Indeed, the discrete structure of spectral lines is a direct consequence of quantum theory. Quite evidently we have to deal here with a highly complicated problem whose solution required new ways of physical thinking. This task has been solved in several steps.

1. Rate equations 

The simplest description which still has the character of a model rests on equations for the temporal change of the numbers of photons with which the individual "cavity" modes are occupied. A typical equation for the photon number n is of the form

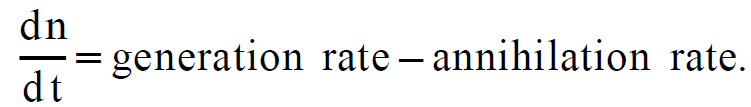
These equations are quite similar to those with which Einstein derived Planck's formula. Such kind of description, which has been used by Tang and Stat z and De Mars and many others for laser processes, is still used today when global phenomena, such as the intensity distribution of laser light, are studied. On the other hand such a model-like description based on photon numbers is insufficient for the treatment of many important processes in modern laser physics. This is in particular so if phase relations between laser light waves are important. A theory which describes most laser processes adequately is the semi classical laser theory.

2. Semi classical theory

This theory deals with the interaction between the electromagnetic Jield of the "cavity" modes and the laser active atoms in solids or gases. The field is treated as a classical quantity, obeying Maxwell's equations, whereas the motion of the electrons of the atoms is treated by means of quantum theory. The source terms in Maxwell's equations, which in a classical treatment stem from oscillating dipoles, are represented by quantum mechanical averages. Furthermore, pumping and decay processes of the atoms are taken into account. The resulting coupled equations are nonlinear and require specific methods of solution. Such a theory was developed in 1962 by myself and was further developed by my coworkers and myself in the subsequent years. This theory, which we shall present in this book in detail, allows us to treat the multimode problem both in solid state as well as in gas lasers. In this way we shall understand under which conditions only a single mode can be selected by the laser process or, when several modes can coexist. Furthermore we shall find that by means of the laser process the frequencies of the emitted laser light are shifted with respect to the atomic and cavity frequencies. Under well-defined approximations, in particular that there are no phase relations between the individual mode amplitudes, the rate equations can be derived from the semi classical equations and thus given a sound basis. A theory equivalent to our theory was developed independently by Lamb and published by him in 1964, whereby Lamb treated the gas laser. A number of important new phenomena, such as ultrashort pulses occur, when phase locking between modes takes place. The semi classical equations are still used by numerous scientists as a basis for the study of various laser phenomena and we shall present a number of explicit examples. In this way, the semi classical theory will form the central part of this book, dealing with the dynamics of laser light.

3. Quantum theory of the laser

The semi classical theory, which describes the behavior of the atoms by means of certain quantum mechanical averages and treats the light field as a classical quantity, has a strange consequence. Whereas above a critical pump power, by which the atoms are continuously excited, laser light is created in the form of a completely coherent wave, below that critical pump strength no light emission should take place at all. Of course, a satisfactory laser theory must contain the emission of usual lamps as a special case also, and it must be capable of explaining the difference between the light from lamps, i.e. from thermal sources, and laser light. As we know, light of conventional lamps is produced by spontaneous emission. Spontaneous emission of light is a typical quantum mechanical process. Quite evidently the semi classical theory cannot treat this process. Thus it becomes necessary to develop a completely quantum mechanical theory of the laser. The previously known quantum mechanical theory, in particular the detailed theory of Weisskopf and Wigner, could explain this spontaneous emission of an individual atom in detail, but this theory was insufficient to describe the laser process. Thus we were confronted with the task of developing a laser theory which is both quantum mechanical and contains the nonlinearities known from semi classical theories. This theory, which I published in 1964, showed that laser light differs basically from light from conventional lamps. Whereas light from conventional lamps consists of individual incoherent wave tracks, laser light essentially consists of a single wave whose phase and amplitude are subject to small fluctuations. Subsequent measurements of the intensity fluctuations of laser light below and above threshold by Armstrong and Smith ( l965), and Freed and Haus (1965) fully substantiated my predictions. My approach required the exclusion of the immediate vicinity of the laser threshold. This gap was closed in 1965 by Risken (and subsequently by Hempstead and Lax). Risken interpreted my quantum mechanical laser equation as a classical Langevin equation and established the corresponding Fokker-Planck equation. The stationary solution of the Fokker-Planck equation describes the photon statistics in the laser. We shall deal with the coherence and noise properties of laser light as well. In order to treat these questions, besides the Langevin and Fokker-Planck equations the density matrix equation was used also. Density matrix equations, which describe both the atoms and the light field quantum mechanically, were derived by Haake and Weidlich (1965), and by Scully and Lamb (1966). Solutions of laser density matrix equations in different kinds of representation were given by Scully and Lamb (1966), and by Weidlich, Risken and Haken (1967). This work was carried further by a number of authors, who used still other representations and included higher order terms.

4. Quantum classical correspondence

In this section we are abandoning the main stream of this book, to which we shall return, 1.2.5, and make some technical remarks of interest to theoreticians. An interesting question arose why a quantum mechanical process can be described by a classical Fokker-Planck equation. This lead to a further development of the principle of quantum classical correspondence which allows us to establish a connection between a quantum mechanical description and a classical formulation without loss of quantum mechanical information. Such a transcription had been initiated by Wigner (1932) who treated quantum systems described by the position and momentum operator. A further important step was done by Glauber and Sudarshan (1963) who treated Bose-field operators. In particular, Glauber's careful study of quantum mechanical correlation functions provided a general frame for the description of the coherence properties of light. But, of course, being a general frame, it did not make any predictions on the coherence properties of laser light. For that purpose, the quantum theory of the laser had to be developed. In it the inclusion of the atomic system is indispensable and required a considerable extension of the principle of quantum classical correspondence which was done by Gordon (1967), and Haken, Risken and Weidlich (1967) along different though equivalent lines. Because the principle of quantum classical correspondence has important applications not only in laser physics but also in nonlinear optics.

5. The laser - trailblazer of synergetics

New vistas on laser theory were opened in 1968 when it was recognized that the transition from light from thermal sources to laser light within an individual laser bears a striking resemblance to phase transitions of systems in thermal equilibrium. Thus the laser became the first example in which the analogy between a phase transition of a system far from thermal equilibrium and one of a system in thermal equilibrium could be established in all details (Graham and Haken, 1968 and 1970; De Giorgio and Scully, 1970; Kasanzev et al. 1968). It soon turned out that there is a whole class of systems which can produce macroscopic ordered states when driven far from thermal equilibrium. This gave birth to a new branch of scientific study, called "synergetics". In this way deep rooted analogies between quite different systems in physics, chemistry, biology and even in the soft sciences could be established. In this new development the laser played the role of a trailblazer. Within the frame of synergetics it became possible to make further predictions on the behavior of laser light. For instance, on account of analogies between fluid dynamics and laser light the phenomenon of laser light chaos was predicted (Haken, 1975). Various routes to chaotic laser light could be discovered experimentally.

6. Optical bistability

In this book we shall include other aspects of laser theory also, for instance that of optical bistability. While in conventional lasers the laser is pumped incoherently, devices leading to optical bistability can be viewed as lasers which are driven coherently by an external field. For this reason a good deal of the theoretical methods developed for the laser can be applied to optical bistability. A thorough theoretical treatment is due to Lugiato and others. The name "optical bistability" stems from the fact that under suitable conditions the transmission of light through a resonator filled with atoms can acquire two different states. The "optical bistability" device bears great promises for the construction of an optical transistor.

7. Two photon laser

The main part of this book deals with laser processes in which an optical atomic transition generates one photon. As we know, in optical transitions also two or several photons can be absorbed or emitted simultaneously. This has led to the idea of a two photon laser to which substantial contributions have been given by Walls, Wang and others.