

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
البوزجاني
المؤلف:
دعنا, عدنان (2010)
المصدر:
معجم علماء الرياضيات
الجزء والصفحة:
131-135
14-8-2016
925
البوزجاني
حياته :
هو أبو الوفاء محمد بن يحيى بن اسماعيل بن العباس البوزجاني، من اعظم رياضي العرب، ومن الذين لهم فضل كبير في تقدم العلوم الرياضية، ولد في بوزجان، وهي بلدة صغيرة بين هراة ونيسابور، في مستهل رمضان سنة 328هـ، قرأ على عمه المعروف بابي عمرو المغازلي، وعلى خاله المعروف بابي عبدالله محمد بن عنبسة، ماكان من العدديات والحسابيات، ولما بلغ العشرين من العمر انتقل الى بغداد حيث فاضت قريحته ولمع اسمه وظهر للناس انتاجه في كتبه ورسائله وشروحه لمؤلفات اقليدس وديوفنطس والخوارزمي.
وفي بغداد قدم ابو الوفاء سنة 370هـ ابا حيان الى الوزير ابن سعدان، فباشر في داره مجالسه الشهيرة التي دون احداثها في كتاب الامتاع والمؤانسة وقدمه الى ابي الوفاء.
وفي بغداد قضى البوزجاني حياته في التأليف والرصد والتدريس، وقد انتخب ليكون احد اعضاء المرصد الذي انشأه شرف الدولة، في سراية، سنة 377هـ، وكانت وفاته في 3 رجب 388هـ على الارجح.
أعماله :
يعتبر ابو الوفاء احد الائمة المعدودين في الفلك والرياضيات، وله فيها مؤلفات قيمة، وقد اعترف له كثير من علماء الغرب بانه من اشعر الذين برعوا في الهندسة، وقال ابن خلكان : له فيه – علم الهندسة – استخراجات غريبة لم يسبق اليها، وكذلك في استخراج الاوتار تصنفي جيد نافع. اما في الجبر فقد زاد على بحوث الخوارزمي زيادات تعتبر اساسا لعلاقة الجبر بالهندسة، وقد حل هندسيا المعادلتين :
س4 = ح، س4 + ح س3 = ب
واستطاع ان يجد حلولا اخرى بالقطع المكافئ، ولا يخفي ان هذه الحلو وغيرها مهدت السبيل لعلماء اوروبا ليتقدموا بالهندسة خطوات قادمت الى التكامل والتفاضل.
وقد اطلع كارادي فو Carra Devaux وسميث Smith وسارطون sarton وغيرهم على بحوث البوزجاني في المثلثات، فأقروا له بالسبق والفضل، واعترفوا بانه اول من وضع النسبة المثلثية (ظل) وانه اول من استعملها في حلول المسائل الرياضية، وقال البيروني : ان الفضل في استنباط هذا الشكل (شكل الظل او المماس) لأبي الوفاء بلا تنازع من غيره.
وادخل البوزجاني القاطع والقاطع تمام، ووضع الجداول الرياضية للمماس، واوجد طريقة جديدة لحساب جدول الجيب، وكانت جداوله دقيقة، حتى ان جيب زاوية 30 درجة كان صحيحا الى ثمانية ارقام عشرية.
ووضع البوزجاني بعض المعادلات التي تتعلق بجيب زاويتين، وكشف بعض العلاقات بين الجيب والمماس والقاطع ونظائرها، واوضح ان :

كما عرف العلاقة الآتية :
ط س : ا – حتا س : حا س

واستعاض عن المثلث القائم الزاوية من الرباعي التام بنظرية منالاوس، مستعينا بما يسمى قاعدة المقادير الاربعة :
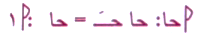
ونظرية الظل :
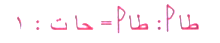
واستخرج هاتين القاعدتين :
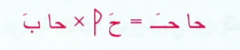
ويقول كارا دي فو ويتحمل انه في المثلث الكروي ذي الزاوية غير القائمة اوجد اولا نظرية الجيب. وكان لجميع هذه المعادلات اثر كبير في تقديم المثلثات، بل كانت فتحا جديدا في عالم الرياضيات، واعترف الطوسي بفضل البوزجاني في المثلثات، واشار الى ذلك في كتابه المشهور شكل القطاع.
على ان ادخال الظل، وظل التمام، والقاطع، وقاطع التمام في حساب المثلثات الكروية كان قد عرفه قبله حبش الحاسب، على حد قول سوتر Suter.
وظهرت عبقرية البوزجاني في نواح اخرى كان لها الاثر الكبير في فن الرسم، فوضع كتابا عنوانه كتاب في عمل المسطرة والبركار والكونيا، وقد ترجمها الغربيون CONSTRUCTION GEOMETRIQUES ويقصد بالكونيا المثلث القائم الزاوية، وفي هذا الكتاب طرق خاصة مبتكرة لكيفية الرسم واستعمال الالات لذلك مما يحتاجه الصانع من اعمال الهندسة ويتألف الكتاب من ثلاثة عشر بابا :
- عمل المسطرة والبركارات.
- في عمل الاشكال في الدوائر.
- في عمل الدائرة على الاشكال.
- في عمل الاشكال بعضها في بعض
- في الاصول والكونيا.
- في عمل الاشكال المتساوية.
- في قسمة المثلثات.
- في قسمة المربعات.
- في عمل مربعات من مربعات وعكسها.
- في قسمة الاشكال المختلفة الأضلاع.
- في الدوائر المتماسة.
- في قسمة الاشكال على الكرة.
- في عمل الدائرة في الاشكال.
من هذه المحتويات تتجلى اهمية الكتاب الذي دفع بأصول الرسم الى الامام، واعرف بذلك علماء تاريخ العلوم. ويلاحظ من دراسة كتاب البوزجاني ان العمليات فيه متنوعة، وان المؤلف استعمل طرقا مختلفة لحل عملية واحدة، وان الكتاب يحتوي على اساليب مبتكرة وطرقاً جديدة لرسم الاشكال والدوائر، وانشاء الاجسام المنتظمة كثير السطوح، حول الكرة، واخذ بعض الغربيين بنظريات رياضية وضعها البوزجاني، فاخلوها في كتبهم، ما فعل ريجومونتانوس في كتابه المثلثات Detriangulis.
واختلف العلماء في نسبة الخلل في حركة القمر، وجرى حول هذا الموضوع نقاش في اكاديمية العلوم الفرنسية في القرن التاسع عشر، فقال بعضهم ان معرفة هذا الخلل ترجع الى تيخو براهي الفلكي الدانمركي المشهور، وبقي المؤرخون تجاه هذا الاختلاف مدة في حيرة، الى ان ثبت لدى الباحثين بعد تحريات دقيقة، ان الخلل الثالث هو من اكتشاف البوزجاني، وان تيخوبراهي ادعاه لنفسه، او نسبة الغير اليه، ولهذا الاكتشاف اهمية كبرى تاريخية وعلمية، لان ادى الى اتساع نطاق الفلك والميكانيكا.
لأبي الوفاء، غير ما ذكر، مؤلفات قيمة، ورسائل نفيسة، منها :
- كتاب ما يحتاج إليه العمال والكتاب من صناعة الحساب وقد اشتهر باسم كتاب منازل في الحساب. وهو سبعة منازل وكل منزلة سبعة ابواب : الاولى في النسبة، الثانية في الضرب والقسمة، والثالثة في اعمال المساحات، الرابعة في اعمال الخراج، الخامسة في اعمال المقاسات، السادسة في الصروف، السابعة في معاملات التجار، وهذا الكتاب كان اساسا لمعاملات الماليين في عصر المؤلف وفي العصور التالية :
- كتاب اقامة البراهين على الدائر من الفلك من قوس النهار طبع في حيدر اباد سنة 1943.
- كتاب تفسير كتاب الخوارزمي في الخبر والمقابلة.
- كتاب المدخل الى الارتماطيقي.
- كتاب فيما ينبغي ان يحفظ قبل كتاب الارتماطيقي.
- كتاب معرفة الدائرة من الفلك.
- كتاب الكامل.
- كتاب استخراج الاوتار.
- كتاب المجسطي وهذا من اثاره المشهورة، ومنه نسخة ناقصة في مكتبة باريس الوطنية، والغالب انه وضع بعد سنة 377هـ.
وخلاصة القول ان البوزجاني ابرع علماء العرب الذين كان لبحوثهم ومؤلفاتهم الاثر الكبير في تقدم العلوم، ولا سيما الفلك، والمثلثات، واصول الرسم، كما كان من الذين مهدوا السبيل لايجاد الهندسة التحليلية، بوضعه حلولا هندسية لبعض المعادلات والاعمال الجبرية العالية
 الاكثر قراءة في علماء الرياضيات
الاكثر قراءة في علماء الرياضيات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















