1.1 Revisiting theorems
The theory of flows in a network, of which we have just developed the bases, is very powerful. It makes it possible, for example, to prove some important theorems as we are going to see with three examples.
1.1.1 Menger’s theorem
Let us recall this theorem in its “vertex statement”: A (undirected) graph G such that n ≥ k +1 is k-connected if and only if any two distinct vertices of G are joined by k internally vertex-disjoint paths (that is pairwise with no other common vertices other than their ends).
The part which is the least easy to prove is the necessary condition. It will easily result from the following lemma which expresses the equality of the value of a maximum flow and of the capacity of a minimum cut in a particular network. This result is in fact the original version of the theorem given by Menger, sometimes called the “local” version of the theorem.
Lemma 1.1. Let G be a simple graph and let x and y be two non-neighboring vertices of G. The greatest number of pairwise vertex-disjoint paths linking x and y in G is equal to the lowest number of elements of a set of vertices A which separates x and y, that is such that x and y are in different connected components of G − A.
Proof. Let us build a network from graph G in the following way: each edge of G is first replaced by two opposite arcs, giving a digraph, denoted by G/, which has the same set of vertices as G. Then, each vertex z ≠x, y of G/is split into two vertices z/and z//with an arc (z/,z//) of capacity 1. Any arc entering into z is replaced by an arc entering into z/with a capacity ∞.Any arc exiting from z is replaced by an arc exiting from z//, also with a capacity ∞. Vertices x and y respectively play the role of source and sink in the network thus defined, which we denote by R (see an example in Figure 1.1).
It is not difficult to verify what follows:
–A flow of R defines a set of pairwise vertex-disjoint paths of G (the arcs of the form (z/,z//) for which the flow takes the value 1 define the corresponding vertices of the paths of G).
– A finite cut of R defines in G a set of vertices A such that x and y are in different connected components of G − A. Indeed, a finite cut of R is necessarily composed of arcs of the form (z/,z//), which are the only arcs with finite capacities and which correspond to vertices of G.
Ford-Fulkerson’s theorem applied to network R then gives the result directly.
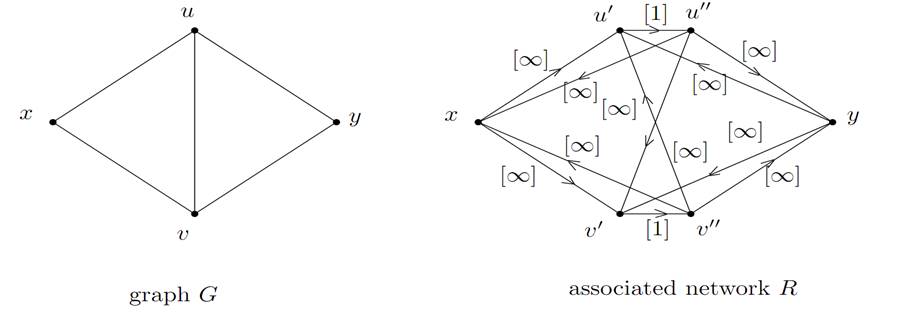
Figure 1.1. Proofoflemma1.1
Let us apply lemma 1.1 to a proof of the necessary condition of Menger’s theorem. Let G be a k-connected graph, let x and y be two vertices of G.
(We may suppose k ≥ 1, the case k = 0 being trivial.) If x and y are not neighbors in G, lemma1.1 gives the result directly. Indeed, the lowest number of elements of a set A, as stated in lemma 1.1, is greater than or equal to the connectedness number of G, κ(G), and G being k-connected we have κ(G) ≥ k. Thus there are a number of vertex-disjoint paths joining x and y at least equal to k .If x and y are neighbors in G, endvertices of an edge e, we can consider graph G−e, which we know to be (k −1)-connected . The application of lemma 8.4 then gives (k − 1)paths joining x and y, which, with the path defined by edge xy and its endvertices, constitute the required number of k paths.
Let us note that we can similarly prove the “edge” version of Menger’s theorem.
1.1.2 Hall’s theorem
Let us recall this classic maximum matching theorem in a bipartite graph: a bipartite graph G =(X, Y,E) allows a matching which saturates X if and only if for any S ⊆ X we have |N(S)|≥|S|, where N(S) designates the set of the neighbors of the vertices of S. The part which is not obvious, the sufficient condition, is an easy consequence of theorem (Gale). A network R, of which X is the set of vertices, with stocks for S defined by σ and with demands on T defined by τ ,allows feasible flow if and only if we have for any U ⊆ X:
c/ω−(U)/≥ τ (T ∩ U) − σ(S ∩ U)). We call the necessary and sufficient condition given in theorem Gale’s condition.
Let us associate with bipartite graph G =(X, Y,E) the transportation network R with stocks and demands, built in the following way. Each edge of G is directed from Y to X and receives a capacity ∞.Set Y is defined as set S of the sources of R, and X as set T of the sinks of R. We define a stock equal to 1 for each source and a demand equal to 1 on each sink. It is easy to see that a feasible flow of R corresponds to a matching which saturates X. The matching is defined by the arcs of R with a flow equal to 1, and, since the demand is satisfied, each vertex of G is in fact saturated by this matching.
It is enough therefore to verify that Hall’s condition in G leads to Gale’s condition in R (a figure may be useful for following the reasoning below).
Let there be U ⊆ X ∪ Y (note that the set of the vertices of the graph here is X ∪ Y , and not simply X as in Gale’s theorem). If we don’t have N(U ∩ X) ⊆ U ∩ Y ,then ω−(U) ≠ ∅, c(ω−(U)) = ∞, and Gale’s condition is trivially verified. If N(U ∩ X) ⊆ U ∩ Y ,we have ω−(U)= ∅,and so c(ω−(U)) = 0, and Gale’s condition can be written:
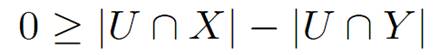
and this condition is really fulfilled since we have:
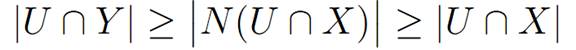
the second inequality being given by Hall’s condition.
1.1.3 König’s theorem
Let us recall this other classic matching theorem ((König). If graph G is bipartite, then ν(G)= τ (G).): if a graph is bipartite, then ν(G)= τ (G), where ν(G) is the maximum of edges of a matching and τ (G) is the minimum of vertices of a transversal of G.
This result is also an equality expression between the value of a maximum flow and the capacity of a minimum cut in a network. Let us build the following network R from bipartite graph G =(X, Y,E). Each edge of G is directed from X to Y and receives capacity ∞. On the one hand we add a vertex s, which will be the single source of the network, and an arc (s, x) with capacity 1 for each x ∈ X. On the other hand, we add a vertex t, which will be the single sink of the network, and an arc (y, t) with capacity 1 for each y ∈ Y . It is not very difficult to verify what follows:
–Aflow of R defines a matching of G and the value of the flow is equal to the number of edges of the matching (consider the arcs of flow equalto 1).
– A finite cut of R defines a transversal of G and the capacity of the cut is equal to the number of vertices of the transversal. Specifically, if the cut of R is defined by the set Z, the transversal of G is (X�)∪(Y ∩Z).
Thus, the value of a maximum flow of R is equal to the number of matching ν(G) and the capacity of a minimum cut of R is equal to the minimum transversal τ (G). Ford-Fulkerson’s theorem then directly gives the equality ν(G)= τ (G)ofKönig’s theorem. The theory of flows in transportation networks presents a remarkable algebraic extension with the concept of tension, dual to that of flow, defined by a
potential function, as in electricity.
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(191-194)
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


