
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تحويلات لورنس
المؤلف:
د. حسون. ناظم احمد ، د. شاحوت. عياد مفتاح و د. ابراهيم. بثينة عبد المنعم
المصدر:
النظرية النسبية الخاصة
الجزء والصفحة:
ص38
26-4-2016
5313
تحويلات لورنس
ان فكرة وجود وسط يملأ كل شيء يسمى الاثير اصبحت لا وجود لها استنادا الى نتائج كثيرة توصل اليها العلماء في هذا الحقل وخاصة تجربة مايكلسن ومورلي. اما اينشتاين ومنذ بداية القرن العشرين وبعد هذه التجربة فقد ادخل اسلوبا جديدا يستند على فرضيتين مهمتين هما :
أولا : ان جميع قوانين الفيزياء متكافئة بالنسبة لجميع محاور الاسناد. اي ان القوانين الخاصة بالفيزياء مثل قوانين نيوتن وغيرها تبقى كما لا تتغير في كل مكان وفي اي زمان.
ثانيا : سرعة الضوء في الفراغ واحدة وتساوي C في جميع محاور الاسناد. اي ان سرعة الضوء ثابتة لجميع المشاهدين ولا تعتمد على أية حركة نسبية للمصدر أو المشاهد.
اذا كانت سرعة الجسيمات عالية تقرب من سرعة الضوء فان تحويلات غاليليو لا تصح في مثل هذه الحالات، فقد لوحظ انها تعطي نتائج غير صحيحة، فجاء لورنس ليدخل تعديلا على هذه التحويلات مستندا على فرضيتي آينشتاين. واقترح ان القياسات المتخذة للإزاحة والزمن بالنسبة لمشاهدي في محور اسناد مختلفين sʹ,s، (حيث ان السرعة النسبية بينهما تساوي v) يجب ان تكتب بالصيغة :
 (1.1)
(1.1)
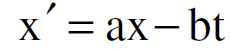 (1.2)
(1.2)
حيث ان b , a معاملان مناسبان ينبغي معرفتهما.
نفرض الان ان محوري الاسناد sʹ,s كانا منطبقين على بعضهما في نقطة اصل مشتركة في زمن t=tʹ=0 وفي هذه اللحظة صدرت اشارة ضوئية في تلك النقطة، كما موضح في الشكل (1.1a).

الشكل (1.1) محور الاسناد sʹ,s a))في حالة انطباقها في زمن t=tʹ=0 b))في حالة انفصالها باتجاه الاحداثي x بعد زمن t ≠ tʹ≠ 0.
وبعد فترة معينة من الزمن t ≠ tʹ≠ 0 يكون المحور sʹ قد انتقل الى موضع جديد باتجاه الاحداثي x كما في الشكل (1.1b)، وخلال تلك الفترة تكون الاشارة الضوئية الاولى قد قطعت في s مسافة باتجاه الاحداثي xمساوية الى :
 (1.3)
(1.3)
وقطعت باتجاه الاحداثي xʹ في محور الاسناد sʹ مسافة مساوية الى :
 (1.4)
(1.4)
وتجدر الاشارة الى ان سرعة الضوء بقيت كما هي مساوية الى .. بالنسبة لمحوري الاسناد (فرضية اينشتاين الثانية). سرعة نقطة الاصل ز. كما هي مقاسة
بالنسبة لمشاهد في s يمكن الحصول عليها بوضع xʹ=0 في المعادلة (1.2) وسرعة نقطة الاصل o كما هي مقاسة بالنسبة لمشاهد في sʹ يمكن الحصول عليها بوضع x=0 في المعادلة (1.1) فيكون :
 (1.5)
(1.5)
الان بتعويض قيمة xʹ من المعادلة (1.4) في المعادلة (1.1) والاستعاضة عن xفي (1.1) بما يساويها في (1.3) ينتج ان :
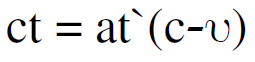
وبالمثل بالنسبة للمعادلة (1.2) يحصل ان :

وبضرب المعادلتين الاخيرتين في بعضهما ينتج ان :

حيث تم اختزال المقدار ttʹ في طرفي المعادلة التي نتجت من عملية الضرب. من العلاقة الاخيرة نحصل على :

وباستبدال العامل a بآخر هو γ :
 (1.6)
(1.6)
اذ ان  .
.
يمكننا كتابة معادلتي التحويل (1.1) و (1.2) كالاتي :
 (1.7)
(1.7)
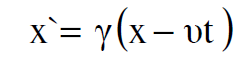 (1.8)
(1.8)
حيث تمثل المعادلة (1.7) تحويل احداثي الازاحة لموقع حدث من sʹ الى s وتمثل (1.8) تحويل احداثي الازاحة من s الى sʹ.
وبما ان محوري الاسناد بينهما حركة نسبية بسرعة ثابتة باتجاه الاحداثي x فان الاحداثيين الاخرين لا يتغير ان خلال عملية التحويل، أي أن :
 (1.9)
(1.9)
بقي لدين الان تحويل الزمن t و tʹ للحصول على معادلتي التحويل بعد الاستعانة بالمعادلتين (1.7) و (1.8).
نعوض عن x في المعادلة (1.8) بما يساويها في المعادلة (1.7) فيكون :

 (1.10)
(1.10)
وبالمثل يمكننا الثبات ان :
 (1.11)
(1.11)
تمثل المعادلة (1.10) تحويل الزمن لحدث ما من محور الاسناد sʹ الى s، وتمثل المعادلة (1.11) تحويل الزمن من s الى sʹ تكتب الان تحويلات لورنس كالاتي
 (1.12)
(1.12)
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















