
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
المتجه الرباعي للزخم وللقوة
المؤلف:
د. حسون. ناظم احمد ، د. شاحوت. عياد مفتاح و د. ابراهيم. بثينة عبد المنعم
المصدر:
النظرية النسبية الخاصة
الجزء والصفحة:
ص145
21-4-2016
3869
المتجه الرباعي للزخم وللقوة
اولا: المتجه الرباعي للزخم.
يعرف الزخم الرباعي بالعلاقة :
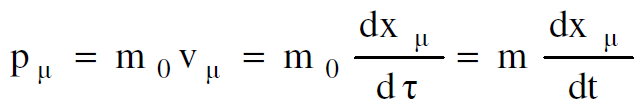 (1.1)
(1.1)
حيث ان Vμ السرعة الرباعية وان m0 الكتلة الساكنة للجسيم. تكتب مركبات هذا المتجه كالآتي :
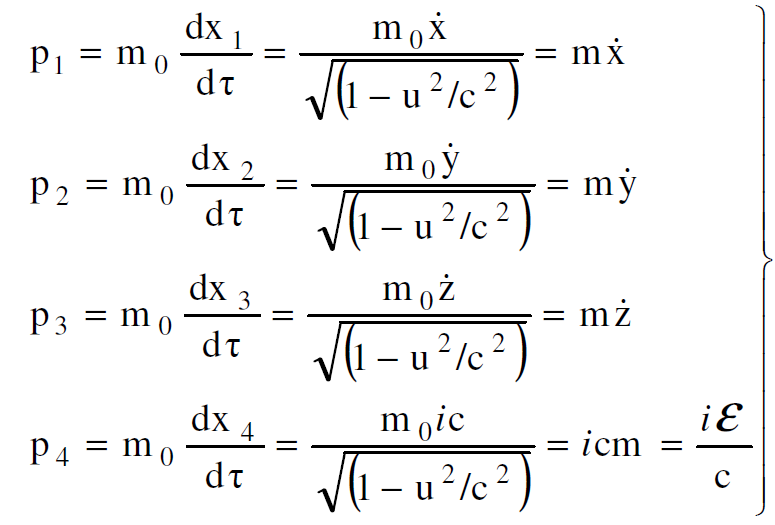 (1.2)
(1.2)
نلاحظ من المعادلات اعلاه ان مركبات الزخم الاعتيادي تشبه تماما مركبات المتجه الرباعي للزخم في الافضاء ذي الابعاد الاربعة ولكن تستعمل هنا الكتلة النسبية بدلا من كتلة السكون.
المتجه الرباعي للزخم يبقى دون تغيير كما يجب ان يكون لأن :
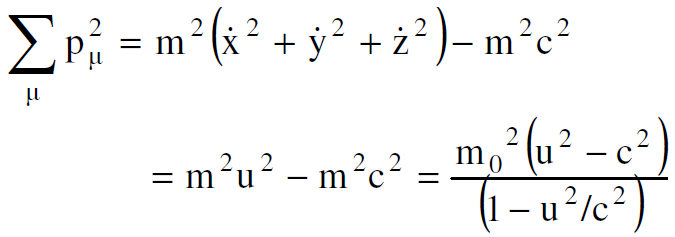
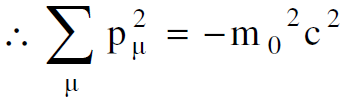 (1.3)
(1.3)
وبما أن هذه الكمية تبقى دون تغيير نكتب :
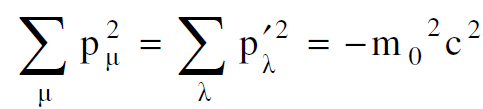 (1.4)
(1.4)
ولما كان الزخم الرباعي يتحول كمتجه رباعي فيمكننا كتابة العلاقة :
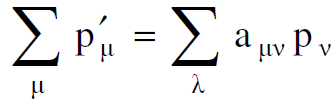 (1.5)
(1.5)
وهكذا تصبح لدينا معادلات التحويل الخاصة بمركبات المتجه الرباعي للزخم :
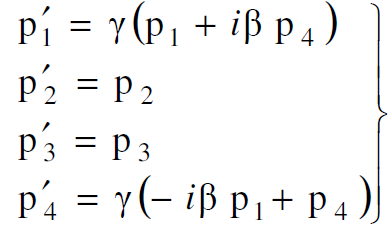 (1.6)
(1.6)
المعادلات (1.2) تكتب بصورة مختصرة على النحو التالي :
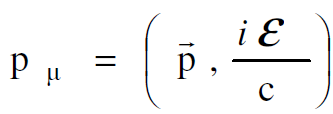 (1.7)
(1.7)
حيث يمثل  متجه الزخم في الفضاء الاعتيادي ومركباته p3, p2, p1 اما المركبة الرابعة فهي
متجه الزخم في الفضاء الاعتيادي ومركباته p3, p2, p1 اما المركبة الرابعة فهي 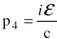 .
.
من العلاقة (1.3) يكون واضحا ان الطاقة الكلية ε يمكن ان يعبر عنها بدلالة الزخم كالآتي :
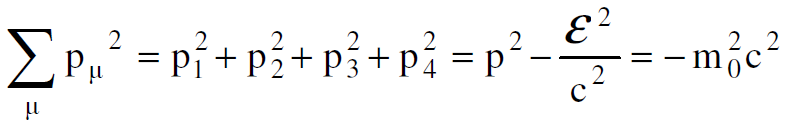
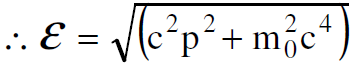 (1.8)
(1.8)
ومن الواضح ايضا من المعادلات (1.7) ان معادلة التحويل الخاصة بالطاقة من محور الاسناد s الى sʹ يمكن الحصول عليها من العلاقة الرابعة اي :
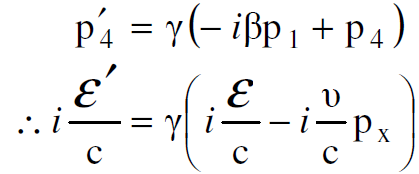
حيث ان : p1=px.
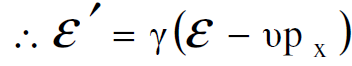
وعلينا ان نذكر ان المتجهات الرباعية وضربها مع بعضها تبقى دون تحت تحويلات لورنس ويمكن ان تستخدم لحل مسائل كثيرة.
نفرض ان طاقة وزخم الجسيم الاول 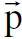 1, ε1 وطاقة زخم الجسيم الثاني 2, ε2
1, ε1 وطاقة زخم الجسيم الثاني 2, ε2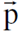 كتلتا سكونهما m02 ,m01 على التوالي. بعد التصادم تكون طاقة وزخم الجسيم الاول
كتلتا سكونهما m02 ,m01 على التوالي. بعد التصادم تكون طاقة وزخم الجسيم الاول 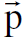 3, ε3 وللجسيم الثاني
3, ε3 وللجسيم الثاني 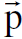 4, ε4 وبتطبيق قانون حفظ الطاقة والزخم خلال عملية التصادم المرن من الممكن استخدام المتجهات الرباعية للزخم كالاتي :
4, ε4 وبتطبيق قانون حفظ الطاقة والزخم خلال عملية التصادم المرن من الممكن استخدام المتجهات الرباعية للزخم كالاتي :
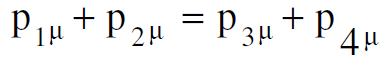 (1.9)
(1.9)
حيث ان:

ومن هذه المعادلات نكون علاقات تبقى دون تغيير تساعد في اجزاء الحسابات المتعلقة بهذه المسألة. ولتوضيح ذلك نعيد كتابة المعادلة (1.9) بالشكل:

وبتربيع طرفي هذه المعادلة يكون لدينا:
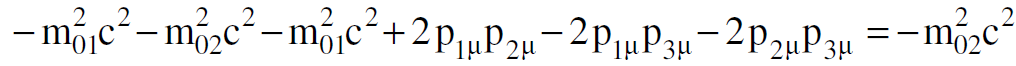
 (1.10)
(1.10)
لنعتبر التصادم قد حصل في محور الأسناد s حيث يلاحظ فيه الجسيم الثاني في حالة سكون قبل التصادم, فيصبح لدينا الان:
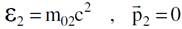
وحاصل الضرب العددي الممثل بالحدود المبينة في المعادلة ( (1.10يساوي:
 (1.11)
(1.11)
حيث ان θ زاوية التشتت للجسيم الساقط (الاول) بعد التصادم وبتعويض هذه العلاقات بالمعادلة ((1.10 ينتج:
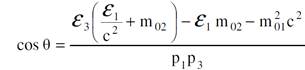 (1.12)
(1.12)
والعلاقة الاخيرة تعطي زاوية التشتت بدلالة طاقة الجسمين في حالة التصادم.
وبإتباع الطريقة نفسها نستطيع ان نكتب علاقة مشابهة فيما يتعلق بزاوية التشتت φ للجسيم الثاني.
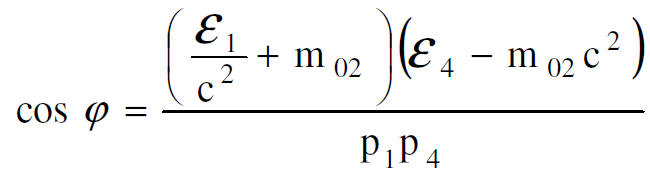 (1.13)
(1.13)
ثانيا : المتجه الرباعي للقوة.
لندخل متجها رباعيا جديدا Fμ يسمى بالقوة الرباعية او المتجه الرباعي للقوة. عندئذ يكون التعميم النسبي لقانون نيوتن الثاني:
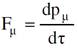 (1.14)
(1.14)
ويمكن كتابة هذه العلاقة بالشكل التالي:
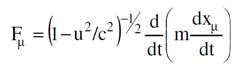 (1.15)
(1.15)
حيث ان 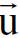 سرعة الجسيم، m الكتلة النسبية. اذن المركبات الثلاثة الاولى للقوة الرباعية تتسب الى القوة الاعتيادي f وتكتب :
سرعة الجسيم، m الكتلة النسبية. اذن المركبات الثلاثة الاولى للقوة الرباعية تتسب الى القوة الاعتيادي f وتكتب :
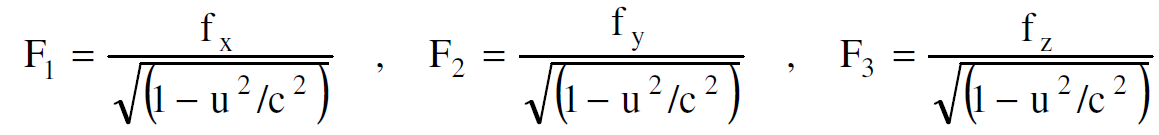
وكذلك بالنسبة للمركبة الرابعة لدينا :
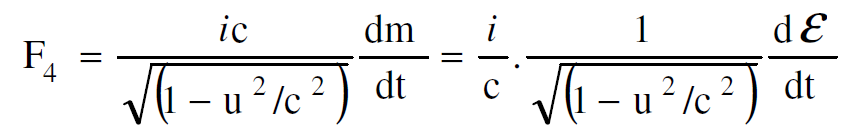 (1.16)
(1.16)
اذن تنسب F4 الى المعدل الزمني الذي تتغير فيه كتلة الجسيم او الكتلة والطاقة. والان بما ان المتجه الرباعي للزخم يبقى دون تغيير اي ان :
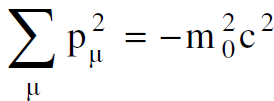
يحصل ان
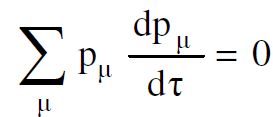
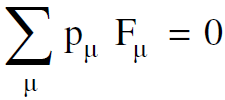 (1.17)
(1.17)
ويمكن تفسير ذلك كصيغة تعامد بين pμ و Fμ وعند كتابة المعادلة (1.17) بصيغة المركبات وجعل اشارة المقدار P4F4 سالبة ينتج :
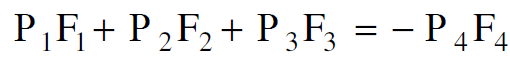
وهذه تكافئ :
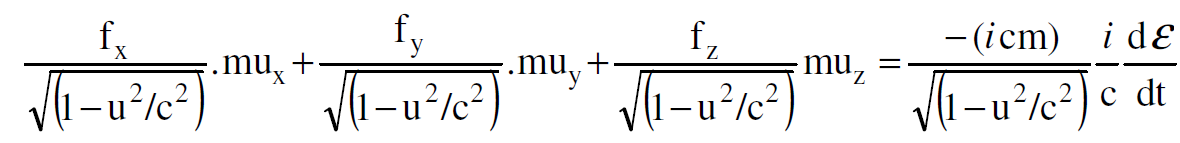
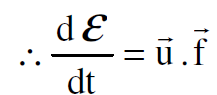 (1.18)
(1.18)
اذن معدل التغير الزمني للكمية ε =mc2 هو المعدل الذي تنجز فيه القوة الاعتيادية 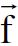 شغلا على الجسيم. وبما ان القوة الرباعية تتحول كمتجه رباعي يمكننا كتابة معادلات التحويل الخاصة بالقوة.
شغلا على الجسيم. وبما ان القوة الرباعية تتحول كمتجه رباعي يمكننا كتابة معادلات التحويل الخاصة بالقوة.
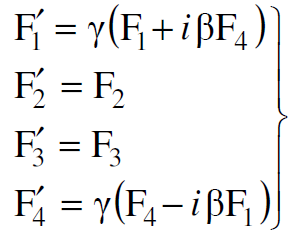 (1.19)
(1.19)
ونوضح الان كيفية استخدام المعادلة الرابعة من (1.19) للحصول على معادلة تحويل الطاقة.
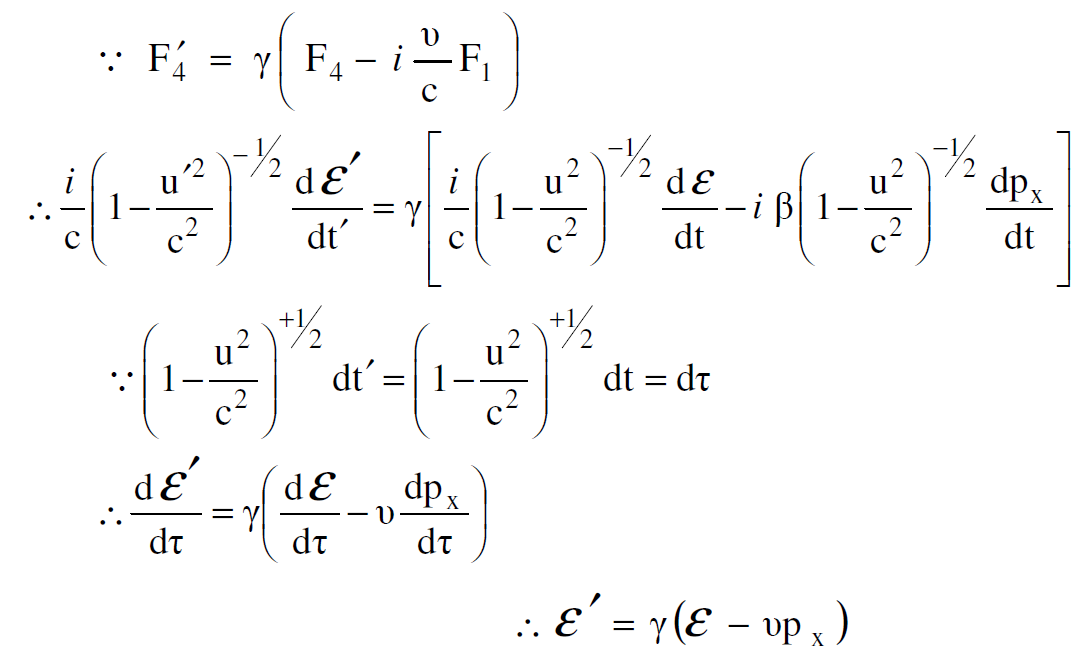
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















