GAUSSIAN   BEAM

The Gaussian output beam (also called a TEM₀₀ beam, signifying that it has the lowest electromagnetic mode structure possible) is, spatially speaking, the purest laser beam possible and is characterized by the lowest divergence of any mode; it is limited only by diffraction. The beam is characterized in intensity in both axes by

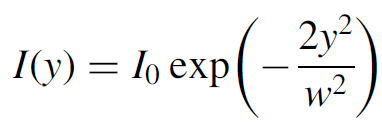 (1.1)

where I₀ is the maximum intensity of the beam, y the distance from the center of the beam, and w the radius of the beam. The intensity profile of the beam is depicted in Figure 1.1. Note from the equation that the radius of the beam (also called the spot size) expands as we move away from the laser, so the calculation of intensity of equation (1.1) applies to a cross section of the beam at an arbitrary distance away from the laser.

       Inside a cavity consisting of two concave mirrors with radius of curvature equal to exactly the distance between them (an arrangement called a symmetric confocal

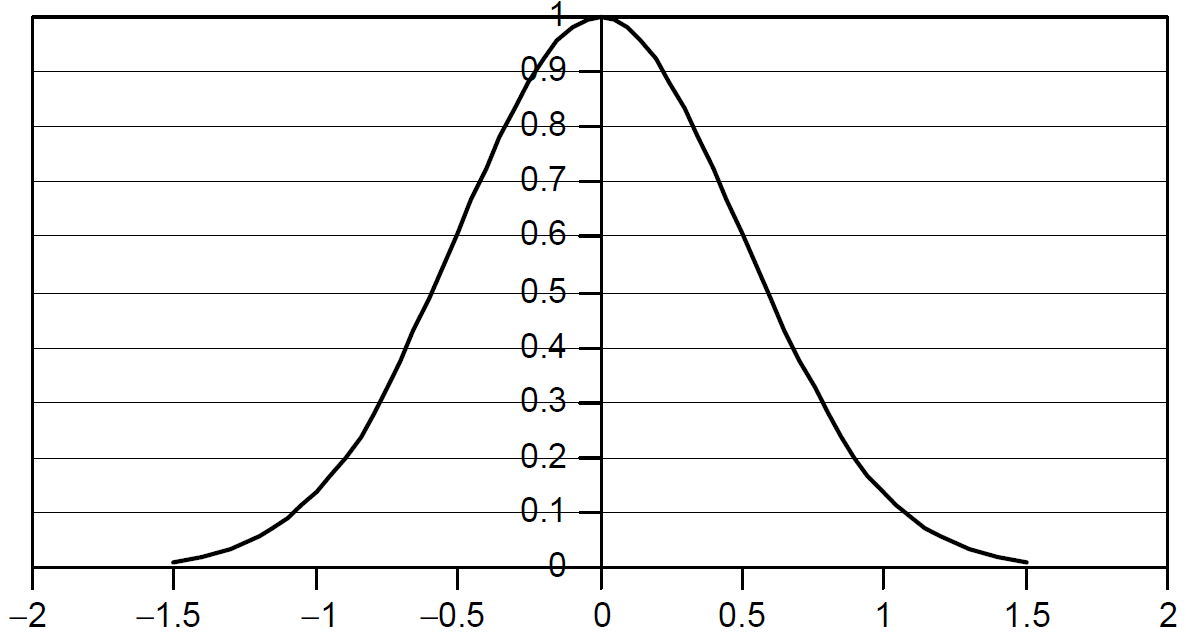
Figure 1.1. Gaussian beam spatial profile.

Figure 1.2. Gaussian beam inside a laser cavity.

resonator and the most general example) the beam converges at the center of the gain medium in what is called the beam waist denoted as w₀ in Figure 1.2. This is the smallest spot size of the beam, and the width of the laser beam at this point is governed by the wavelength and the separation of the cavity mirrors according to

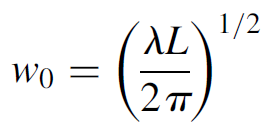 (1.2)

where λ is the wavelength of the laser and L is the distance between the cavity mirrors. It should also be noted from Figure 1.2 that the volume of the amplifier utilized in the laser process is not the entire volume of the gain medium. A Gaussian beam in a laser cavity does not utilize the entire lasing volume and will hence not render the highest output power for a given laser. Higher-order modes, covered later in this chapter, can often utilize the gain medium more effectively than a Gaussian (TEM₀₀) beam can.

      Inside the cavity, the wave fronts of the Gaussian beam do not stay constant but rather, deviate. At the beam waist wave fronts are plane, but as they move toward the cavity mirrors the shape changes to match that of the radius of curvature of the mirrors essentially that of a spherical wave. Wave fronts exiting the laser through

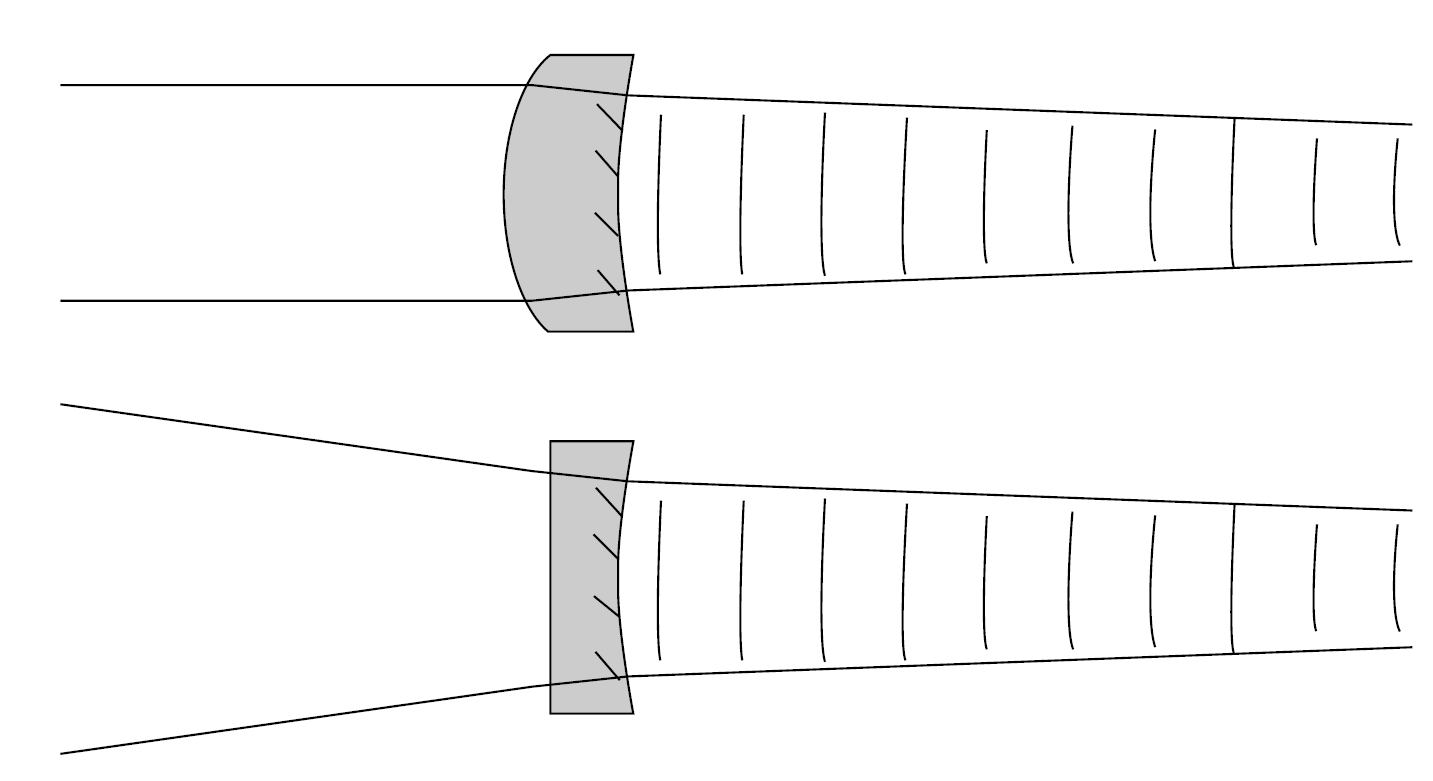
Figure 1.3. Collimating lenses used with lasers.

the output coupler also have this characteristic shape, and upon exiting through the OC diverge at an angle of

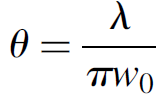 (1.3)

where θ is the half-angle of the divergence. This formula is derived from the radial expression for a Gaussian beam, which is a complex (i.e., involving a complex term -j) expression. The angle 2θ then defines a cone which contains 86% of the power of the laser beam. Note that this approximation does not apply to beams close to the waist since it is a simplified expression with neglected terms. It is entirely valid outside the cavity, however, so defines the divergence of the exit beam. Since divergence is a function of wavelength as well as beam waist, laser beams are inherently more collimated if they are of shorter wavelengths and have large beam waists (e.g., in the case of a large gain medium). This explains why shorter wavelength (e.g., UV) lasers have a distinct advantage in performing delicate cutting and high-resolution photolithography applications requiring small spot sizes (as well as why next-generation CDs and DVDs will use shorter wavelength lasers than the infrared lasers currently in use). Regardless of the wavelength, however, the beam will continue to diverge after exiting the laser, the divergence made even worse by the fact that the output coupler itself will act as a lens. To collimate the beam, most lasers use either an external collimating lens or, more frequently (especially compact lasers such as He Ne tubes with integral tube mirrors), the outer surface of the output coupler itself is shaped as a convex lens, as depicted in Figure 1.3.