Computer Simulation of Biological Molecules

Biological molecules are systems of enormous complexity. This makes it exceedingly difficult to elucidate the details of biological activities using only experimental techniques. Despite enormous progress in structural studies of proteins, it is hard to determine uniquely how the particular function is determined by the given structure. A mathematical description of the energy of a macromolecule in terms of its atomic coordinates is, in principle, sufficient to predict relevant biological properties. However, such a description can only be handled by powerful computers. Having the proper model of a macromolecule should allow one to simulate its properties as if one is dealing with the actual molecule. Such an approach, called computer simulation, offers what is probably the best way of describing the function of macromolecules.

 The relationship between the energy of molecules and the position of its atoms is called a potential function or a force field. A reasonable potential function provides the first step for modeling a molecule. In principle, one can obtain potential functions by using quantum mechanical methods that describe the entire molecule as a supermolecule. However, such methods are not yet practical for describing macromolecules. Some progress can be made using hybrid QM/MM approaches, but, in general, it is essential to use approximated potential functions whose parameters are based on empirical information (1-5).

Potential functions can be based on all-atom molecular models that describe the interactions between all the atoms of the given molecule or on simplified models where the forces due to several atoms are described by a single interaction center. Examination of molecular properties using the corresponding potential functions is known as molecular mechanics. This term is usually reserved for the use of energy minimization and normal mode analysis methods. The use of potential functions to solve the equation of motion of atoms is known as molecular dynamics (MD). This method gives the atomic position as a function of time and provides a powerful way of obtaining dynamical and time average properties. In some cases one can obtain useful insight by using Brownian dynamics. Frequently it is sufficient to know the properties of macromolecules at their minima. Generating starting configurations in the search for such minima can be done by Monte Carlo methodsMonte Carlo calculations and other sampling approaches. Apparently, the most important biological properties are reflected in most cases by thermodynamic properties and not dynamical properties. In particular the Free Energy provides the most important connection between structure and function, while the knowledge of the individual contributions to free energy from enthalpy and entropy is less critical for reproducing functional properties of macromolecules. The free energy of macromolecules can be evaluated by several approaches and, in particular, by the free energy perturbation (FEP) and linear response approximation (LRA) methods. Free energy calculations are frequently based on the use of thermodynamic cycles (3, 4, 6).

The potential functions that describe the energetics of macromolecules reflect different types of interactions. This includes bonding and van der Waals interactions that determine the steric properties of the given molecule and electrostatic interactions (that include hydrogen bonding and other dipolar and ionic interactions). The free energy of macromolecules is largely dependent on electrostatic energies, which reflect the effect of polar and ionized groups and its compensation by the polarization of the solvent around the protein (6, 7). These energies involve long-range interactions, whose accurate evaluation present a major challenge. Electrostatic energies can be modeled by using implicit models where the solvent molecules (and sometimes the protein dipoles( are represented implicitly. The use of a dielectric constant in an electrostatic model is a form of implicit model, and, in fact, the dielectric constant in many electrostatic models is not related at all to the true protein dielectric constant but to the properties that are not simulated explicitly (6, 8). Computer simulations of biological molecules has been particularly effective in studies of the following subjects.

1. Energetics (Thermodynamics and Equilibrium Properties(

Simulation of the free energies of different biological processes provide the “missing link” between the corresponding structures and functions. This is particularly true with regard to electrostatic free energies. However, obtaining reliable free energies by computer simulations is very challenging and requires validation by discriminative benchmarks. One of the most effective test in of calculations of free energies in proteins in general and electrostatic models in particular is provided by calculations of absolute pK_as of ionizable groups in proteins (8). The basis for calculating this quantity is the relationship (6)

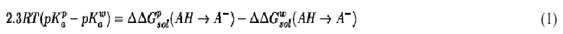
where the superscripts p and w denote protein and water, respectively, and DDG_sol(AH → A^–) is the difference in solvation energy between the protonated and deprotonated states of the acid. Although early models only considered the change of pK_as due to the effect of protein ionized groups (9), it is now recognized that the most important factor is the self-energy (6) (or “solvation energy”), which is the energy of forming the charge in its protein environment when the other charges are turned off. The modulation of this effect is largely determined by the protein permanent dipoles (6). Obtaining reliable estimates of the self-energy by Free Energy Perturbation is very challenging, but significant progress has been made (3, 10). Apparently, it is essential to treat long-range effects in a consistent way in order to obtain meaningful results in pK_a calculations (10). It is frequently simpler to obtain better results by simplified solvent models (6) and by models that treat the solvent as a dielectric continuum (11). However, one must bear in mind that models that treat the protein in a uniform dielectric without considering the microscopic nature of the protein permanent dipoles cannot reproduce the correct physics of ionized groups in proteins (6, 8).

Redox energies of biological cofactors play a major role in electron transfer processes. Such energies can be evaluated by simulation methods using a similar approach to that used in equation 1 and evaluating the change in solvation energy upon moving the charge from water to the protein. FEP calculations of redox energies were reported by several workers, and related studies in  photosynthetic reaction centers were also presented. Here the proper treatment of the solvent around the protein is quite crucial (12). As in the case of pK_a calculations, one finds that simplified models (13) and continuum models (14, 15) are quite effective.

Reliable calculations of free energies of ligand binding are crucial for quantitative progress in rational drug design. FEP has been used extensively in studies of binding free energies (3). Most early studies involve simple cases of small changes in the ligand (16). Calculations of absolute binding free energies are much more challenging (3, 17) and involve major convergence problems. Here the use of the LRA has been found to be quite effective (17-19). Extensive progress has also been made with simplified models (17, 19, 20) and with more phenomenological approaches (21, 22).

The permeation of ions through membrane channels plays a major role in biophysics. Here, the challenge is in evaluating the energy of an ion in the channel relative to its energy in solution and using the energetics in determining the conductance of the channel. Reliable simulation of such systems requires one to properly represent the channel and its surrounding membrane and water environment. The energy contribution of the membrane-induced dipoles must be included in consistent calculations. Consistent FEP studies of the energetics of moving an Na⁺ ion to the center of the gramicidin A channel have been reported with a reasonable result (23). Incomplete modeling of the boundaries of the simulated system and long-range interactions can lead to significant overestimates of the penetration barrier (eg, the results of ref. 24). Semimacroscopic studies of ion channels are quite useful and much less challenging than full microscopic calculations (10, 25, 26). The recent emergence of the structure of a bacterial potassium channel (27) have highlighted the need for reliable FEP calculations, and some progress has been already made (28).

2. Structural Properties

 Molecular simulations can be used to refine, and sometimes predict, structural properties. Energy minimization approaches were the first to be used successfully in relaxing bad steric contacts in X-ray crystallography (29). Such approaches were also used in more systematic refinements of protein structures (30). The emergence of powerful computers allows one to use more rigorous statistical mechanical approaches coupled with MD simulations in exploring structural properties (31).

Simulations are also very useful in evaluating and analyzing temperature factors and interpreting the meaning of the corresponding experimental results.

All-atom simulation approaches are still quite ineffective in predicting protein-structures, and one has to resort to simplified models. Even when one starts from the X-ray structure, it is not trivial to have the simulated structure identical to the observed one. The problems involved include the need for reliable potential function and, perhaps more importantly, the need to have a realistic description of the solvent (32) and proper treatment of long-range forces.

3. Dielectric Properties

 Although proteins cannot and should not be described as a medium of a uniform dielectric constant, it is important to understand the dielectric properties of proteins. Experimental attempts to determine local dielectric constants are far from being unique, and simulation studies can provide great insight. In relating the simulated dielectric constant to experimental observations, one should take into account the effect of the solvent around the protein, which is also referred to as the reaction field (33) . Consistent simulations of the overall dielectric constant of solvated proteins have been reported by several workers (34-36). It has been found that the local dielectric at protein active sites is quite large and quite different than the low value usually deduced from dielectric measurements (37). Simulations are also very effective in analyzing the fast time components of dielectric relaxation times (34, 36).

4. Dynamical Properties

 MD simulations and related approaches provide powerful ways of evaluating dynamical properties. Many of these properties can be casted in terms of the corresponding time correlation function (38).

where A is the property of interest and t is a sufficiently long simulation time. For example, the diffusion constant, D, can be obtained from the velocity autocorrelation, Cv(t), by 

This relationship can be used in comparing simulations to experiments and in analyzing the microscopic meaning of experimentally deduced parameters. The dynamical range accessible to simulation studies can be probed by several approaches, and significant progress has been made in comparing simulations to the results of inelastic neutron scattering (39.(

 Molecular fluctuations are characterized by correlation times, which are closely related to the underlined relaxation processes. Relevant relaxation times can be evaluated by simulation studies using: 

The fluctuations of the macroenvironments of proteins can play an important role in fast reactions. This is true in particular with regard to the effect of electrostatic fluctuations on charge transfer processes such as electron transfer reactions. The rate of such reactions is determined by the effect of the protein fluctuation on the difference between the energies of the reactant and product state. Such an approach has been used in studies of the dynamics of the primary event in photosynthesis 26, 40-42. The same approach can be used in studies of photoisomerization processes, although in such cases one needs to account for a large coupling between the electronic states. As much as rate constants of regular chemical reactions are concerned, the most important factors are activation energies  and not dynamical effects. Nevertheless, the chance that a trajectory that reaches the transition state will lead to reaction of the transmission factor is a dynamical effect. This factor can be evaluated using MD simulation by running trajectories downhill from the transition state (43) (Fig. 1). However, the transition factor is usually close to unity in reactions with significant activation barrier (4, 26) (Fig. 1).

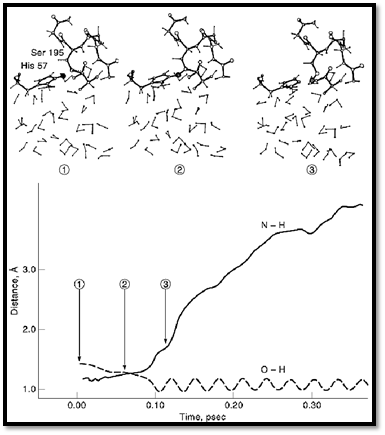
Figure 1. A downhill trajectory for the proton transfer step in the catalytic reaction of trypsin. The trajectory moves on the actual ground state potential, from the top of the barrier to the relaxed enzyme–substrate complex. 1, 2, and 3 designate different points along the trajectory, whose respective configurations are depicted in the upper part of the figure. The time reversal of this trajectory corresponds to a very rare fluctuation that leads to a proton transfer from Ser 195 to His 57. (adapted from ref. 4).

5. Rate of Biological Processes

 The rate constant of processes in condensed phases can be expressed as: 

where k_B is the Boltzmann constant, T is the absolute temperature, h is the Planck constant, F is the transmission factor of section 3, and Dg‡ is the activation-free energy. For most reactions with large Dg‡, one finds that F is close to unity and, thus, the most important factor is Dg‡. Enzymes catalyze their reactions by reducing activation-free energies (44), and one of the most important questions in structure function correlation is how this reduction of Dg‡ is accomplished (4).

Molecular simulations should allow one to evaluate activation free energies and transmission factors and to probe the molecular origin of enzymatic reactions. However, such reactions involve bond making and bond making processes that cannot be described by simple force fields. It is also impractical to describe the complete enzyme/substrate complex by high level quantum mechanical approaches. A possible alternative is provided by hybrid Quantum mechanics/molecular mechanics (hybrid QM/MM) methods 4, 45-49. Such methods describe only parts of the reacting system quantum mechanically, while treating the rest of the protein classically. QM/MM approaches are very promising, but the corresponding results are not yet quantitative (26). An alternative, which is, at present, the most reliable way of simulating enzymatic reaction, is provided by the Empirical Valence Bond (EVB) approach (4, 26, 50, 51). The EVB method describes the reaction potential surface by a valence bond method that considers the different resonance structures of the reactant and product fragments and their interaction with the surrounding protein and solvent. This method is calibrated by considering the reference reaction in water so that it focuses on the difference between the reaction in protein and solution, which is much easier to obtain than to predict the reaction potential surface in the protein by a first principle approach.

The EVB approach can be used to calculate conveniently and efficiently activation-free energies of enzymatic reactions using a combination of FEP and umbrella sampling approaches (4, 50). The activation energies can be converted to rate constants of enzymatic reactions using equation 5.

6. Protein Folding

Models that use simplified representation of the protein amino acids (52) have provided a powerful understanding of the protein folding process (53-56). Such models are sometimes classified as on-lattice and off-lattice models. On-lattice models consider the simplified representation along a regular cubic lattice (thus allowing exact enumeration at the expense of somewhat unrealistic structure), while the off-lattice models try to provide more realistic representation (52). Simplified models are used extensively in understanding the relationship between sequence to folding probability and to the specific folded structure (52-56) and in deducing the sequence of events in the folding process (53). The gradual increase in computer power makes it tempting to use all-atom simulations in studies of folding processes. Some advances have been made (57-59), and more will follow. A promising effective approach is the use of the simplified representation as a reference potential for all-atom calculations (60).

References

1. S. Lifson and A. Warshel (1968) J. Chem. Phys. 49, 5116. 

2. U. Burkert and N. L. Allinger (1982) Molecular Mechanics, American Chemical Society, Washington, DC. 

3. P. Kollman (1993) Chem. Rev. 93, 2395–2417. 

4.A. Warshel (1991) Computer Modeling of Chemical Reactions in Enzymes and Solutions John Wiley & Sons, New York. 

5. A. T. Hagler, E. Huler, and S. Lifson (1977) J. Am. Chem. Soc. 96, 5319. 

6. A. Warshel and J. Åqvist (1991) Ann. Rev. Biophys. Chem. 20, 267–298. 

7. P. E. Smith and B. M. Pettitt (1994) J. Phys. Chem. 98, 9700–9711. 

8. C. N. Schutz and A. Warshel (2001) Proteins: Struc., Func., and Gen. 44, 400–417. 

9. C. Tanford and J. G. Kirkwood (1957) J. Am. Chem. Soc. 79, 5333. 

10. F. S. Lee, Z. T. Chu, and A. Warshel (1993) J. Comp. Chem. 14, 161–185. 

11. B. Honig, K. Sharp, R. Sampogna, M. R. Gunner, and A. S. Yang (1993) Proteins: Struc., Func., and Gen. 15, 252–265. 

12. R. G. Alden, W. W. Parson, Z. T. Chu, and A. J. Warshel (1995) J. Am. Chem. Soc. 117, 12284-12298.

13. P. J. Stephens, D. R. Jollie, and A. Warshel (1996) Chem. Rev. 96, 2491.

14. M. R. Gunner and B. Honig (1991) Proc. Natl. Acad. Sci. U.S.A. 88, 9151–9155. 

15.  H-; X. Zhou (1994) J. Am. Chem. Soc. 116, 10362–10375. 

16. T. P. Straatsma and J. A. McCammon (1992) Ann. Rev. Phys. Chem. 43, 407–435. 

17. F. S. Lee, Z. T. Chu, M. B. Bolger, and A. Warshel (1992) Prot. Eng. 5, 215–228. 

18. J. Åqvist, C. Medina, and J.–E Samuelsson. (1994) Prot. Eng. 7, 385–391. 

19.n Y. Y. Sham, Z. T. Chu, H. Tao, and A. Warshel (2000) Proteins: Struct. Funct. Genet. 39, 393–407.

20. N. Froloff, A. Windemuth, and B. Honig (1997) Protein Sci. 6, 1293–1301. 

21. G. Verkhivker, K. Appelt, S. T. Freer, and J. E. Villarfranca (1995) Prot. Eng. 8, 677–691. 

22.I. Muegge and Y. C. Martin (1999) J. Med. Chem. 42, 791–804. 

23.J. Åqvist and A. Warshel (1989) Comments Mol. Cell Biophys. 6, 91.

24.B. Roux and M. J. Karplus (1993) Am. Chem. Soc. 115, 3250–3260. 

25.V. Dorman, M. B. Partenskii, and P. C. Jordan (1996) Biophys. J. 70, 121–134. 

26.A. Warshel and W. W. Parson Quart. Rev. Biophys. In Press. 

27.D. A. Doyle, J. M. Cabral, R. A. Pfuetzner, A. L. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait, and R. MacKinnon (1998) Science 280, 69–77. 

28.V. Luzhkov and J. Aqvist (2001) Biochimica et Biophysica Acta 36446, 1–9. 

29.M. Levitt and S. J. Lifson (1969) J. Mol. Biol. 46, 269–279. 

30. A. Jack and M. Levitt (1978) Acta Cryst. A 34, 931. 

31.A. T. Brunger (1988) XPLORE Manual, 1.5 ed., Yale University, New Haven, CT. 

32.M. Levitt and R. Sharon (1988) Proc. Natl. Acad. Sci. U.S.A. 85, 7557–7561. 

33. L. J. Onsager (1936) Am. Chem. Soc. 58, 1486. 

34. G. King, F. S. Lee, and A. J. Warshel (1991) Chem. Phys. 95, 4366–4377. 

35. T. Simonson and D. J. Perahia (1995) Am. Chem. Soc. 117, 7987. 

36.W. F. vanGunsteren and A. E. Mark (1992) Eur. J. Biochem. 204, 947.

37.  A. Warshel and A. Papazyan (1998) Curr. Opin. Struct. Biol. 8, 211–217. 

38.D. A. McQuarrie (1976) Statistical Mechanics, Harper and Row, New York. 

39. S. Cusack (1989) Chemica Scripta 29A, 103–107. 

40. A. Warshel and W. W. Parson (1991) Annu. Rev. Phys. Chem. 42, 279–309. 

41.  S. Creighton, J.–K. Hwang, A. Warshel, W. W. Parson, and J. Norris (1988) Biochemistry 27, 774-781.

42. K. Schulten and M. Tesch (1991) Chem. Phys. 158, 421–446. 

43. C. H. Bennet (1997) Algorithms for Chemical Computations, ACS, Washington, DC. 

44. L. Pauling (1946) Chem. Eng. News 263, 294. 

45. A. Warshel and M. Levitt (1976) J. Mol. Biol . 103, 227–249. 

46. V. Théry, D. Rinaldi, J.-L. Rivail, B. Maigret, and G. G. Ferenczy (1994) J. Comp. Chem. 15, 269-282.

47. J. Gao (1995) Reviews in Computational Chemistry, Vol. 7, VCH, New York. 

48. A. J. Mulholland, G. H. Grant, and W. G. Richards (1994) Prot. Eng. 6, 133–147. 

49. R. B. Murphy, D. M. Philipp, and R. Friesner (2000) J. Comput. Chem. 21, 1442–1457. 

50. J. Åqvist and A. Warshel (1993) A. Chem. Rev. 93, 2523–2544. 

51. J. Lobaugh and G. A. Voth (1996) J. Chem. Phys. 104, 2056–2069. 

52.M. Levitt and A. Warshel (1975) Nature 253, 694. 

53. J. N. Onuchic, P. G. Wolynes, Z. Luthey-Schulten, and N.D. Socci (1995) Proc. Natl. Acad. Sci. U.S.A. 92, 3626–3630.