

Grammar


Tenses


Present

Present Simple

Present Continuous

Present Perfect

Present Perfect Continuous


Past

Past Simple

Past Continuous

Past Perfect

Past Perfect Continuous


Future

Future Simple

Future Continuous

Future Perfect

Future Perfect Continuous


Parts Of Speech


Nouns

Countable and uncountable nouns

Verbal nouns

Singular and Plural nouns

Proper nouns

Nouns gender

Nouns definition

Concrete nouns

Abstract nouns

Common nouns

Collective nouns

Definition Of Nouns

Animate and Inanimate nouns

Nouns


Verbs

Stative and dynamic verbs

Finite and nonfinite verbs

To be verbs

Transitive and intransitive verbs

Auxiliary verbs

Modal verbs

Regular and irregular verbs

Action verbs

Verbs


Adverbs

Relative adverbs

Interrogative adverbs

Adverbs of time

Adverbs of place

Adverbs of reason

Adverbs of quantity

Adverbs of manner

Adverbs of frequency

Adverbs of affirmation

Adverbs


Adjectives

Quantitative adjective

Proper adjective

Possessive adjective

Numeral adjective

Interrogative adjective

Distributive adjective

Descriptive adjective

Demonstrative adjective


Pronouns

Subject pronoun

Relative pronoun

Reflexive pronoun

Reciprocal pronoun

Possessive pronoun

Personal pronoun

Interrogative pronoun

Indefinite pronoun

Emphatic pronoun

Distributive pronoun

Demonstrative pronoun

Pronouns


Pre Position


Preposition by function

Time preposition

Reason preposition

Possession preposition

Place preposition

Phrases preposition

Origin preposition

Measure preposition

Direction preposition

Contrast preposition

Agent preposition


Preposition by construction

Simple preposition

Phrase preposition

Double preposition

Compound preposition

prepositions


Conjunctions

Subordinating conjunction

Correlative conjunction

Coordinating conjunction

Conjunctive adverbs

conjunctions


Interjections

Express calling interjection

Phrases

Sentences


Grammar Rules

Passive and Active

Preference

Requests and offers

wishes

Be used to

Some and any

Could have done

Describing people

Giving advices

Possession

Comparative and superlative

Giving Reason

Making Suggestions

Apologizing

Forming questions

Since and for

Directions

Obligation

Adverbials

invitation

Articles

Imaginary condition

Zero conditional

First conditional

Second conditional

Third conditional

Reported speech

Demonstratives

Determiners


Linguistics

Phonetics

Phonology

Linguistics fields

Syntax

Morphology

Semantics

pragmatics

History

Writing

Grammar

Phonetics and Phonology

Semiotics


Reading Comprehension

Elementary

Intermediate

Advanced


Teaching Methods

Teaching Strategies

Assessment
Problems of relational features
المؤلف:
MANFRED BIERWISCH
المصدر:
Semantics AN INTERDISCIPLINARY READER IN PHILOSOPHY, LINGUISTICS AND PSYCHOLOGY
الجزء والصفحة:
423-24
2024-08-16
1195
Problems of relational features
Having settled provisionally the problem of arguments and their delimitation, we return to the predicative features. We already mentioned that these are to be classified in part according to the number of their arguments. This then raises questions of the following type: is there an upper limit for the number k of k-place predicates to be included in the inventory of basic semantic elements? Is there a fixed number of arguments for each predicate or are there those with a varying number of arguments? We will see furthermore that predicative features may differ not only with respect to the number, but also to the type of arguments. Let us consider these problems by means of some examples.
It is obvious from the foregoing discussion that the number of arguments of a predicative feature must be somehow connected to the number of NPs required by the lexical entry whose reading contains that feature. Thus the verbs ‘hit’ and ‘give’, for example, are often considered as expressing two- and three-place relations, respectively, ‘ buy ’ and ‘ sell ’ on the other hand as expressing relations with two, or three, or even four arguments:
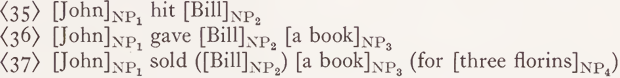
The fact that ‘give’ requires three NPs to form a non-elliptic sentence, however, does not imply that its reading contains a three-place predicate. In fact, it has been shown by Bendix (1966) that the meaning of ‘give’ should be analyzed into two two-place relations in the following way:
(38) C causes (A has B)
where C represents the referent of the subject-NP, B that of the direct object, and A that of the indirect object. If we assume that XS, XD, and X1 represent variables of a dictionary reading to be substituted by the Xi of the subject, direct object, and indirect object respectively, then (38) can be replaced by (39):
(39) [Cause] XS ([Have] X1 XD)
Such a combination of features, where the second argument of the predicate Causation is not a variable over a set of individuals but a proposition, raises several problems that will be discussed later.
With respect to ‘ buy ’ and ‘ sell ’, Katz (1967) has proposed an analysis that reduces the apparent four-place relation essentially to a combination of several two-place features of the form ‘X possesses Y’ with varying arguments and different time specifications, thus characterizing the process of exchange of goods and money between the subject and the indirect object referent of ‘ buy ’ and ‘ sell There are several possibilities to represent the necessary time specifications. One of them is the introduction of an abstract relation ‘ [R]t(P) ’ where t is a variable over time intervals and P a proposition representing a process or a state occurring at time t. With this convention we can represent Katz’ analysis of ‘ sell ’ in the following way, using XF as the variable to be substituted by the XA of the prepositional phrase with ‘ for ’:
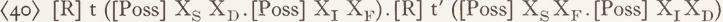
The time interval t' immediately follows t1.
What I have tried to show by means of these examples, which could easily be extended, is that many - if not all - lexical entries requiring or admitting three or more NPi are to be analyzed into appropriate combinations of two-place features. Thus the number k of possible arguments for elementary predicative features can certainly be strongly restricted. In fact, one might hypothesize that in general only one- and two-place relations are required.2
It seems reasonable furthermore to assume that each particular feature always has the same number of arguments. The varying number of NPs permitted in sentences such as (37) does not imply that there are features with a varying number of arguments, but merely that some of these arguments are not specified by additional lexical items and thus do not appear in the surface structure in the form of separate constituents. (Whether a lexically unspecified argument must leave at least a pronoun as its trace or whether it can be dropped altogether or left un¬ specified even in the deep structure representation is part of the syntactic characterization of particular lexical items.)
We must now consider somewhat more detailed features like ‘ Caus ’, which take propositions as one of their arguments. First of all, the existence of such features leads to a further classification of features, which, then, must be specified not only with respect to the number, but also the type of their arguments. Though ‘Caus’ and ‘ Have ’ are both two-place relations, they belong obviously to different types of features. This classification, however, must be specified still further. Consider the following sentences:
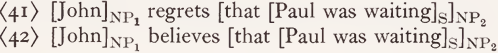
The reading of ‘regret ’ and ‘ believe ’ must contain, among other things, relational features representing a certain attitude of their first argument - the X1 provided by the NP1 ‘John’ in (41) and (42) - towards their second argument, provided by the complement ‘that Paul was waiting’.
These features, which we may abbreviate by ‘ Believe ’ and ‘ Regret ’ for the sake of simplicity, are similar to ‘ Caus ’ in that they take a proposition as their second argument. But whereas ‘ Believe ’ represents indeed an attitude towards a proposition, viz. that the individuals represented by the first argument are inclined to take it as a true proposition, ‘ Regret ’ represents an attitude not towards a proposition, but towards a fact represented by the proposition in question. In this respect, ‘ Caus’ must be classed with ‘ Regret’, as it is the fact described by its argument proposition, not that proposition itself, which is brought about by the first argument of ‘ Caus’. Thus ‘John gave Mary some juice’ does not mean that John causes the proposition expressed by ‘ Mary has some juice ’, but the fact represented by that proposition. Let us call features of the ‘ Caus ’ and ‘ Regret ’ type ‘ fact-features ’ - or for short ‘ F-features ’, and those of the ‘ Believe ’ type ‘proposition-features’ or ‘P-features’. It seems to me that the difference between F-features and P-features is closely connected to the problem which Reichenbach (1966, pp. 268-74) tries to explicate by means of so-called fact variables. For every proposition, Reichenbach claims, there may be a fact such that the proposition describes that fact.3 This suggests that P-features take a proposition as their second argument, whereas F-features take the name of a fact.4 The difference between these two types of arguments must be represented explicitly for both syntactic and semantic reasons. For syntactic consequences I refer to Kiparsky and Kiparsky (1970). The revealing distinction between Factive and Non-factive predicates proposed there has at least one of its most important sources in the distinction of F-features and P-features. (It would be premature to claim that both distinctions are identical, though one might at least look for arguments in this direction.) Among the semantic reasons for the necessity of an explicit distinction between factive and propositional arguments are at least the problems of negation and of opaque contexts. As to the first problem, there are several of the P-features/where the negation of that feature and of its argument are synonymous, whereas no such possibility exists for F-features. A rough illustration is given by the negations of <42):
(43) (a) John does not believe that Paul was waiting.
(b) John believes that Paul was not waiting.
(44) (a) John does not regret that Paul was waiting.
(b) John regrets that Paul was not waiting.
Whereas the sentences under (43) are synonymous, those under (44) are obviously not. I cannot go into the details here of the problems involved, a characterization of those P-features which have the property in question and those which have not, etc.
The problem of opaque contexts can be stated - with many oversimplifications - as follows. Given two propositions P1 and P2 which are logically equivalent, but not synonymous. (We might say that P1 and P2 describe in a sense the same fact but in different ways.) Then a context is opaque, if P1 cannot be substituted for P2 salva veritate.5
Assume, for example, that, given a certain setting, ‘Paul was waiting’ is true if and only if ‘Paul was wasting his time’ is true. Then both sentences describe the same fact. In this case, (46) is true if and only if (42) is true, whereas (45) might be false, even though (41) is true, and vice versa:
(45) John believes that Paul was wasting his time.
(46) John regrets that Paul was wasting his time.
Hence (41) is an opaque context, while (42) is not. The relevant fact is that P- features can constitute opaque contexts, while F-features cannot.
It follows from these remarks that a formal explication of the distinction in question and a suitable notation to represent it depends on several problems of semantic representations. Most of these problems are scarcely understood, to say nothing about their solution. If I nevertheless propose a tentative notation, it is only in order to facilitate some additional remarks. What any account of the problem in question must provide seems to be the following: given a proposition P, i.e. a well defined combination of delimiting and predicative features with suitable arguments, the name of the fact associated with P must be derivable. Using the notation proposed so far, we may write this name as ‘ (Def Xi) ([P]Xi)’.6 The way in which such a fact name provides the argument for an F-feature depends on whether alternative (i) or (ii) discussed above with respect to the operators (QXi) is accepted. Let P be the reading of ‘Paul was waiting’ and ‘(Def X1) ([J]X1)’ the reading of ‘John1’. Assume furthermore that the reading of ‘regrets’ consists only of the F-feature ‘Regret’, then we get (47) and (48), corresponding to (23) and (24) respectively, as the reading of (41):
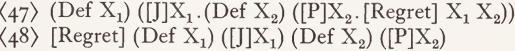
The propositional argument of a P-feature, on the other hand, can be represented by the proposition itself. Assuming that the reading of ‘ believe ’ consists only of the feature ‘Believe’ (and its argument variables), we get either (49) or (50) as the reading of (42):
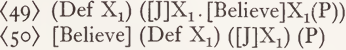
Consider now the hypothesis of Paul and Carol Kiparsky (1969) that the complements of Factive and Non-factive predicates have the underlying structure (51 a) and (51 b), respectively:

This assumption, motivated by several syntactic phenomena, suggests that the noun ‘fact’ of (51 a) has semantically the effect of deriving the fact name corresponding to the proposition expressed by S. In other words, the reading of ‘the fact’ in one of its meanings has the form ‘(Def Xi) ([P]Xi)’ where P is a variable over propositions to be substituted by the reading of the complement sentence and i is the reference index of the dominating NP-node. This seems to me a fairly reasonable account of the semantic connection between ‘the fact’ and its attributive clause in (52 a), which is unlike that of the restrictive clause to ‘the fact’ in
(52 b):

It must now be noted that fact arguments appear not only in the syntactic function of complements to Factive verbs or adjectives, but also within the readings of single lexical items. The reading of ‘give’ is an obvious example. (39) must therefore be reformulated as:
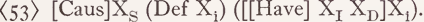
The fact in question is represented here by Xi. Similarly, propositional arguments occur both as explicit complements and as internal elements of lexical readings. An example of the latter would be ‘esteem’ in one of its readings. This might be given as:

where ‘High Value’ is short for features representing positive evaluation.
So far we have discussed problems of relational features occurring in the readings of verbs. These considerations apply directly to adjectives governing objects, e.g. ‘free’, ‘due’, etc., or complements, such as ‘eager’, ‘able’, etc. I will now touch briefly on relational features occurring in readings of relational nouns such as ‘father’, ‘friend’, ‘side’, ‘roof’, etc. Nouns of this type express social roles, the part-whole-relation, etc. Semantically the representation of such relations is straightforward, by means of such two-place predicates as ‘Parent’, ‘Part’, etc. The problem here is the syntactic index required for the variables in the lexical reading. Notice first of all that every noun must contain in its lexical reading a variable which is to be replaced by Xi, if the noun in question functions as the head noun of an NPi. This variable will be indexed for the relation ‘ Subject-of’, since it is precisely this variable which is to be substituted by the argument expression provided by the subject NP, if a noun is used in the predicate NP of a copula sentence. The question then is: what is the syntactic index of the second argument occurring in relational nouns? This question is directly related to the problem of the structure underlying such NPs as ‘John’s father’, ‘the left side of a chair’, etc. It has been assumed, at least implicitly, by many writers that possessive genitives should be derived from underlying relative clauses with ‘have’. T. his seems to me quite unnatural, however, in the case of inherent relations pertinent to relational nouns of the type discussed here. It seems more reasonable to assume that relational nouns ‘govern’ an object NP in much the same way as verbs and adjectives do. Thus the structure underlying ‘John’s father’ should be something like
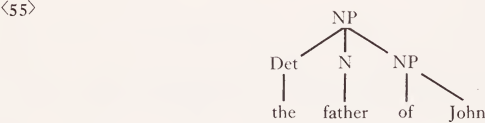
A similar proposal has recently been made by Fillmore (1968).7 If we abbreviate the syntactic function of an attributive NP of the type in question by the index G, the reading of ‘ father ’ can be given as:

From this lexical reading, (58) can be derived as the semantic interpretation of
(57):
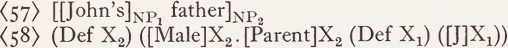
An example of unalienable possession would be ‘hand’, whose lexical reading is given in (59) with ‘Hand’ as an abbreviation for a rather complex set of semantic features:

1 This analysis is oversimplified and in many respects not relevant for the present discussion. Thus I ignore here and throughout this paper the problem of selection restrictions or presuppositions. In fact, the lexical reading of ‘ sell ’ must contain at least the following selectional features: ‘ [Human] XS. [Human] X1. [Money] XF. [Physical Object v Artifact] XD’. I doubt, furthermore, that Katz’ analysis is correct, insofar as it is based on the assumption that ‘buy’ and ‘sell’ are in a sense inverse relations, i.e. that (i) and (ii) are synonymous sentences:
(i) John sold Bill a book, (ii) Bill bought a book from John.
This claim would imply that (iii) and (iv) are also synonymous:
(iii) Bill was sold a book, (iv) Bill bought a book.
But that this is at least controversial can be seen from the following examples:
(v) Bill was sold a book in order to give it to Mary.
(vi) Bill bought a book in order to give it to Mary.
Therefore (40) should be replaced, presumably, by something like:
(vii) [R] t ([Poss] XS XD. [Poss] X1 XF).[R] t ([Caus] XS ([Poss] XS XF. [Poss] X1 XD)) See Katz (1967) and Bierwisch (1969) for further discussion. Notice incidentally that also ‘give’ must contain a time specification. Thus (39) should be rendered into (viii):
(viii) [R] t ([Caus] XS ([Have] X1XD)).
2 An apparent counterexample to this speculation is the preposition ‘ between ’ and its equivalents in other languages:
(i) John1 was seated between Bill2, Paul3, Sam4. . ., and Petern.
Sentences like
(ii) John1 was seated between them7
suggest, however, that NP2 through NPn in (i) must be analyzed as dominated by a single NP, whose reference index is 2 + 3+4+...+n. The corresponding variable X2+3+. . .+n would then be the second argument of the feature characterizing ‘ between’, just as X7 is its second argument in (ii). If this assumption is right, ‘ between ’ would contain a two-place predicate which requires its second argument variable to be a set of more than one object.
3 Reichenbach introduces the following notation: p ≡ (ꓱ v) p* (v). In other words: p is true if and only if there is a fact v such that v is described by p. The asterisk on p transforms the proposition p in a predicate assigned to a fact variable. Since this p uniquely specifies a particular fact, the name of that fact can always be given by means of a definite description: (‘ v) p* (v), meaning ‘the fact that p’.
4 Actually the distinction between fact arguments and proposition arguments, discussed here with respect to relational features, need not be restricted to these. There may be one-place predicates taking propositions and fact names respectively as their only arguments. Adjectives like ‘important’, ‘odd’, ‘tragic’, etc. in one of their readings contain one-place F-features, ‘true’, ‘possible’, etc. corresponding P-features. The same holds for verbs like ‘count’ and ‘seem’, respectively. I am somewhat cautious with respect to one-place F- and P-features, because it is not a priori clear whether most of the relevant items do not contain an implicit second argument representing the speaker of the utterance. This means that it might turn out that ‘That he comes, is true’ must be analyzed as something like ‘The proposition expressed by “he comes” is true for me’. Notice, incidentally, that F-features and P-features need not necessarily be disjoint sets. There may be features taking alternatively propositions and fact names as arguments.
5 The problem of opacity has been discussed mainly in connection with believe-sentences. See e.g. Carnap (1964) and references quoted therein.
6 This notation is, of course, analogous to that of Reichenbach mentioned in note a, p. 425, above as I have argued earlier that the operator (Def X) corresponds, mutatis mutandis, to (‘ x). I omit the asterisk of Reichenbach’s notation, since in fact a confusion cannot arise.
 الاكثر قراءة في Semantics
الاكثر قراءة في Semantics
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















