The structure of paths

Before proceeding to a criticism of the notion of projection rules in KF, we have to consider further the algebra of the dictionary entries.

If a dictionary entry, conceived of as a paradigmatic tree, has the form (i2i), where A, B, C, D, E, and F are semantic features, there is no reason against reformulating it as (12 ii)

(provided the convention is maintained that all such trees are read ‘ downwards ’). We have already alluded to such cases of reconvergence in the semantic path after branching in the syntactic path, and many examples come to mind of strictly semantic reconvergence, e.g. (13). But it will be noticed that there is no a priori order for the markers.

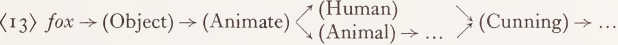
Suppose we stipulate that, in a given dictionary, the markers A, B, C, ..., if they occur in the same entry, appear in alphabetical order; then the subpaths A-C-D-G and B-C-H of same entry would be conflated as (14). If, on the other hand, we require (by a metatheoretical convention) that all reconvergence of branches be avoided, the proper form of the complex entry would be perhaps as in (15).

At any rate, it may be useful to realize in advance that the criteria of a fixed order of markers and a fixed form of branching may be mutually irreconcilable.

In contrast to the syntagmatic trees representing the structure of sentences, the purely paradigmatic trees corresponding to polysemous dictionary entries are under no constraints on Analyzability in the sense e.g. of Chomsky and Miller (1963 : 301). Hence the descriptive problem reduces itself to finding the most economical path-work, with a minimum of repetition of features. By exemplifying the problem with trees which are representable as pure taxonomies, KF gives an oversimplified view of the problem. Thus, a classificatory tree such as (16 i), in which A, B, C, Q, R, S, and T are features and a path of features connected by lines constitutes a meaning, is equivalent to (16 ii), which explicitly represents it as a taxonomy:

However, many dictionary entries tend to the form of matrixes of features, as in (17 i), and there is no motivated reason to rewrite them as (17 ii); the only economy would be achieved by representations such as (17 iii-v):

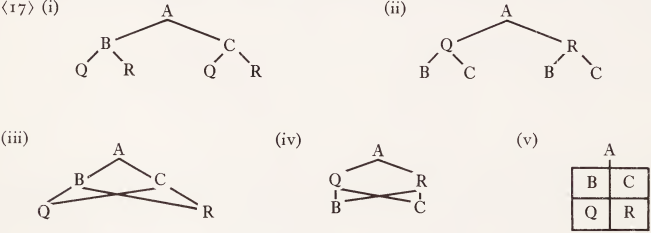
In short, unprejudiced reflection leads to the conclusion that no theoretical motivation is in prospect for specifying the order of features in a path.¹

A related difficulty arises when we observe the amalgamation of paths which results from the operation of the projection rules. Given the dictionary entries, with their respective paths, W_a = a₁ + a₂+ ... +a_m and W_b = b₁ + b₂+ ... + b_n, the compound lexical string W_a + W_b has the compound path a₁ + a₂ + ... + a_m + b₁ + b₂+ ... + b_n; but there is no formal representation of the juncture between that portion of the compound path which came from W_a and that which came from W_b. In KF the distinguishers of W_a, if any, appear at the point where the constituent paths of an amalgamated path have been joined ;² but as we have seen, this is purely arbitrary with respect to the theory. In fact, the origin of each marker in an amalgamated path is not recoverable; the elements of an amalgamated path in KF, like those of the constituent paths, are strictly unordered sets, and there is no way, valid within the theory, of saying that in the path of W_a + W_b, a_m (for example) precedes  b₁.

Let us consider some consequences of this property of KF. Given the separate paths for the English words detective and woman, the constructions woman detective and detective woman would be represented by identical amalgamated paths, since the order of elements in a path, and hence of subpaths in a path, is theoretically immaterial. KF turns out, in other words, to be unable to represent the interchange of foregrounded and backgrounded information in such pairs.³ But the dilemma, though awkward, is still relatively benign, since the semantic effect of rearranging the constituents is of very limited significance. A far more pernicious weakness of the theory appears when one considers that the two sentences in (18) would also receive identical semantic interpretations (‘readings’). The paths of (1) cats, (2) chase, and (3) mice -

(18) (i) Cats chase mice.

(ii) Mice chase cats.

although amalgamated in the order 1 + (2 + 3) in (18 i) and as (2 + 1) + 3 in (18 ii) - would yield the same unordered set of features, (1 2 3), as the amalgamated path; for, as we have seen, there is neither ordering nor bracketing of elements in a KF path. For similar reasons, the theory is unable to mark the distinction between three cats chased a mouse and a cat chased three mice, between (bloody + red)+ sunset and bloody + red+ sunset, and so on for an infinite number of crucial cases.

For KF, the meaning of a complex expression (such as a phrase or a sentence) is an unstructured heap of features -just like the meaning of a single word. The projection rules as formulated in KF destroy the semantic structure and reduce the words of a sentence to a heap. Very far from matching a fluent speaker’s interpretation of sentences or explicating the way in which the meaning of a sentence is derived from the meaning of its components, KF only hints at the presence, in some unspecified capacity, of some meanings somewhere in the structure of a sentence. It tells us, in effect, that (18i) is an expression which says something about cats, mice and chasing', and that (18 ii) does likewise.

It might, of course, be countered that while the set of semantic features in both sentences of (18) is the same, the grammar of these expressions is different. But this is precisely the issue: how is the difference in grammar concretely related to the difference in total meaning? On this KF is silent. What is particularly ironic is that an enterprise in semantics inspired by the most sophisticated syntactic research ever undertaken should end up with a fundamentally asyntactic theory of meaning. In its inability to distinguish (18i) from (18 ii), KF is comparable to certain (linguistically useless) psychological accounts of sentences which seek to explain the meaning of a sentence in terms of ‘ associations ’ between its component words.⁴

To avoid similar defects in an alternative theory, it may be useful to consider how KF maneuvered itself into a position of bankruptcy on the most essential issue. Apparently, this happened when the authors modeled a theory of linguistic meaning on the concept of the multiplication of classes. As logicians have long known, to express the fact that a colorful ball is something which is both colorful and a ball, we may say that colorful ball contains the semantic features of both ball and colorful. The process involved in deriving a compound meaning is expressible as a Boolean class conjunction. One would have thought that with the development of the calculus of many-place predicates, the logic of Boolean (one-place) predicates would be permanently dropped as a model for natural language; yet KF persists in the belief, widespread among nineteenth-century logicians, that Boolean operations are an adequate model for combinatorial semantics. The dire results of such a belief are evident.⁵

¹ The prospect that implicational relations among markers, such as those discussed by Katz and Postal (1964) and Chomsky (1965), may automatically yield unique networks of features, is attractive, but it is unlikely to be borne out when non-anecdotal evidence is considered.

² E.g. on p. 201, under P8, but not consistently (e.g. not on p. 198), and not in accordance with the formal rule stated on p. 198.

³ Reanalysis of these transformed expressions into their underlying sentences, e.g. The detective is a woman vs. The woman is a detective, would not resolve matters, since the addition of the same ultimate components can only lead to the same results in the total.

⁴ For a relatively recent attempt, cf. Mowrer (i96o), ch. 4.

⁵ Among linguistic theories growing out of logic, KF is thus a distinct step backward from Reichenbach (1948), who realized the need for the higher functional calculus in a semantic theory applicable to natural languages. But Reichenbach himself was antiquated when compared to Stohr (1898), who had already appreciated the necessity of supplementing the functional calculus by other models. The logically irreducible character of transitivity was also a continuing interest of Peirce’s (e.g. 3.408, and in many other places in his work).