Now we come to another interesting proposition. Suppose that we have a certain particular driving force F_a (let us say an oscillatory one with a certain ω=ω_a, but our conclusions will be true for any functional form of F_a) and we have solved for the forced motion (with or without the transients; it makes no difference). Now suppose some other force is acting, let us say F_b, and we solve the same problem, but for this different force. Then suppose someone comes along and says, “I have a new problem for you to solve; I have the force F_a+F_b.” Can we do it? Of course we can do it, because the solution is the sum of the two solutions x_a and x_b for the forces taken separately—a most remarkable circumstance indeed. If we use (25.3), we see that

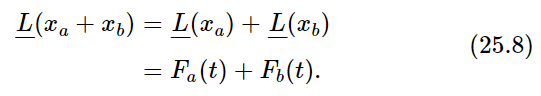
This is an example of what is called the principle of superposition for linear systems, and it is very important. It means the following: if we have a complicated force which can be broken up in any convenient manner into a sum of separate pieces, each of which is in some way simple, in the sense that for each special piece into which we have divided the force we can solve the equation, then the answer is available for the whole force, because we may simply add the pieces of the solution back together, in the same manner as the total force is compounded out of pieces (Fig. 25–1).

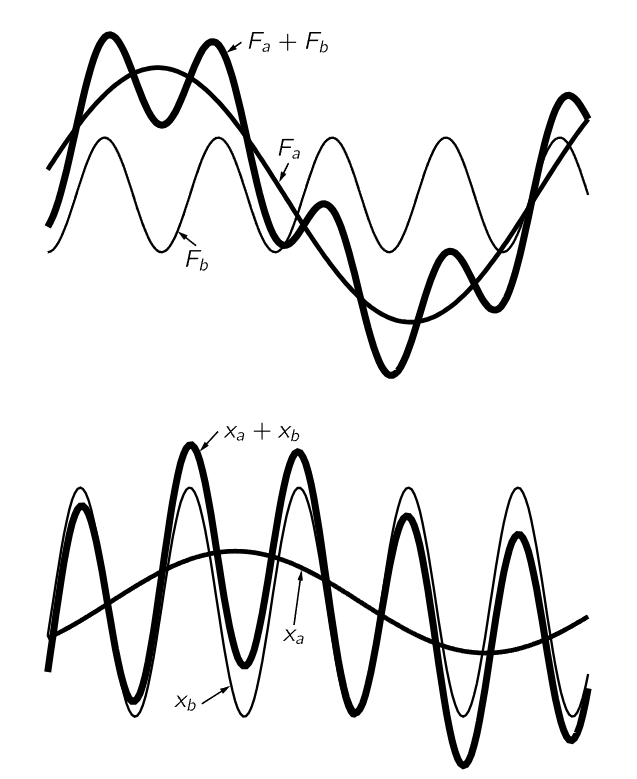
Fig. 25–1. An example of the principle of superposition for linear systems.

Let us give another example of the principle of superposition. It was one of the great facts of the laws of electricity that if we have a certain distribution of charges q_a and calculate the electric field E_a arising from these charges at a certain place P, and if, on the other hand, we have another set of charges q_b and we calculate the field Eb due to these at the corresponding place, then if both charge distributions are present at the same time, the field E at P is the sum of E_a due to one set plus E_b due to the other. In other words, if we know the field due to a certain charge, then the field due to many charges is merely the vector sum of the fields of these charges taken individually. This is exactly analogous to the above proposition that if we know the result of two given forces taken at one time, then if the force is considered as a sum of them, the response is a sum of the corresponding individual responses.

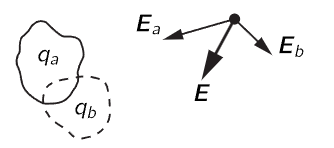
Fig. 25–2. The principle of superposition in electrostatics.

The reason why this is true in electricity is that the great laws of electricity, Maxwell’s equations, which determine the electric field, turn out to be differential equations which are linear, i.e., which have the property (25.3). What corresponds to the force is the charge generating the electric field, and the equation which determines the electric field in terms of the charge is linear.

As another interesting example of this proposition, let us ask how it is possible to “tune in” to a particular radio station at the same time as all the radio stations are broadcasting. The radio station transmits, fundamentally, an oscillating electric field of very high frequency which acts on our radio antenna. It is true that the amplitude of the oscillation of the field is changed, modulated, to carry the signal of the voice, but that is very slow, and we are not going to worry about it. When one hears “This station is broadcasting at a frequency of 780 kilocycles,” this indicates that 780,000 oscillations per second is the frequency of the electric field of the station antenna, and this drives the electrons up and down at that frequency in our antenna. Now at the same time we may have another radio station in the same town radiating at a different frequency, say 550 kilocycles per second; then the electrons in our antenna are also being driven by that frequency. Now the question is, how is it that we can separate the signals coming into the one radio at 780 kilocycles from those coming in at 550 kilocycles? We certainly do not hear both stations at the same time.

By the principle of superposition, the response of the electric circuit in the radio, the first part of which is a linear circuit, to the forces that are acting due to the electric field F_a+F_b, is x_a+x_b. It therefore looks as though we will never disentangle them. In fact, the very proposition of superposition seems to insist that we cannot avoid having both of them in our system. But remember, for a resonant circuit, the response curve, the amount of x per unit F, as a function of the frequency, looks like Fig. 25–3. If it were a very high Q circuit, the response would show a very sharp maximum. Now suppose that the two stations are comparable in strength, that is, the two forces are of the same magnitude. The response that we get is the sum of x_a and x_b. But, in Fig. 25–3, x_a is tremendous, while x_b is small. So, in spite of the fact that the two signals are equal in strength, when they go through the sharp resonant circuit of the radio tuned for ω_a, the frequency of the transmission of one station, then the response to this station is much greater than to the other. Therefore, the complete response, with both signals acting, is almost all made up of ω_a, and we have selected the station we want.

Fig. 25–3. A sharply tuned resonance curve.

Now what about the tuning? How do we tune it? We change ω₀ by changing the L or the C of the circuit, because the frequency of the circuit has to do with the combination of L and C. In particular, most radios are built so that one can change the capacitance. When we retune the radio, we can make a new setting of the dial, so that the natural frequency of the circuit is shifted, say, to ω_c. In those circumstances we hear neither one station nor the other; we get silence, provided there is no other station at frequency ω_c. If we keep on changing the capacitance until the resonance curve is at ω_b, then of course we hear the other station. That is how radio tuning works; it is again the principle of superposition, combined with a resonant response.²

To conclude this discussion, let us describe qualitatively what happens if we proceed further in analyzing a linear problem with a given force, when the force is quite complicated. Out of the many possible procedures, there are two especially useful general ways that we can solve the problem. One is this: suppose that we can solve it for special known forces, such as sine waves of different frequencies. We know it is child’s play to solve it for sine waves. So we have the so-called “child’s play” cases. Now the question is whether our very complicated force can be represented as the sum of two or more “child’s play” forces. In Fig. 25–1 we already had a fairly complicated curve, and of course we can make it more complicated still if we add in more sine waves. So it is certainly possible to obtain very complicated curves. And, in fact, the reverse is also true: practically every curve can be obtained by adding together infinite numbers of sine waves of different wavelengths (or frequencies) for each one of which we know the answer. We just have to know how much of each sine wave to put in to make the given F, and then our answer, x, is the corresponding sum of the F sine waves, each multiplied by its effective ratio of x to F. This method of solution is called the method of Fourier transforms or Fourier analysis. We are not going to actually carry out such an analysis just now; we only wish to describe the idea involved.

Another way in which our complicated problem can be solved is the following very interesting one. Suppose that, by some tremendous mental effort, it were possible to solve our problem for a special force, namely an impulse. The force is quickly turned on and then off; it is all over. Actually, we need only solve for an impulse of some unit strength, any other strength can be gotten by multiplication by an appropriate factor. We know that the response x for an impulse is a damped oscillation. Now what can we say about some other force, for instance a force like that of Fig. 25–4?

Fig. 25–4. A complicated force may be treated as a succession of sharp impulses.

Such a force can be likened to a succession of blows with a hammer. First there is no force, and all of a sudden there is a steady force—impulse, impulse, impulse, impulse, … and then it stops. In other words, we imagine the continuous force to be a series of impulses, very close together. Now, we know the result for an impulse, so the result for a whole series of impulses will be a whole series of damped oscillations: it will be the curve for the first impulse, and then (slightly later) we add to that the curve for the second impulse, and the curve for the third impulse, and so on. Thus, we can represent, mathematically, the complete solution for arbitrary functions if we know the answer for an impulse. We get the answer for any other force simply by integrating. This method is called the Green’s function method. A Green’s function is a response to an impulse, and the method of analyzing any force by putting together the response of impulses is called the Green’s function method.

The physical principles involved in both of these schemes are so simple, involving just the linear equation, that they can be readily understood, but the mathematical problems that are involved, the complicated integrations and so on, are a little too advanced for us to attack right now. You will most likely return to this some day when you have had more practice in mathematics. But the idea is very simple indeed.

Finally, we make some remarks on why linear systems are so important. The answer is simple: because we can solve them! So most of the time we solve linear problems. Second (and most important), it turns out that the fundamental laws of physics are often linear. The Maxwell equations for the laws of electricity are linear, for example. The great laws of quantum mechanics turn out, so far as we know, to be linear equations. That is why we spend so much time on linear equations: because if we understand linear equations, we are ready, in principle, to understand a lot of things.

We mention another situation where linear equations are found. When displacements are small, many functions can be approximated linearly. For example, if we have a simple pendulum, the correct equation for its motion is

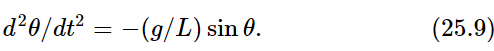
This equation can be solved by elliptic functions, but the easiest way to solve it is numerically, as was shown in Chapter 9 on Newton’s Laws of Motion. A nonlinear equation cannot be solved, ordinarily, any other way but numerically. Now for small θ, sin θ is practically equal to θ, and we have a linear equation. It turns out that there are many circumstances where small effects are linear: for the example here the swing of a pendulum through small arcs. As another example, if we pull a little bit on a spring, the force is proportional to the extension. If we pull hard, we break the spring, and the force is a completely different function of the distance! Linear equations are important. In fact they are so important that perhaps fifty percent of the time we are solving linear equations in physics and in engineering.

__________________________________________
Margin

2- In modern superheterodyne receivers the actual operation is more complex. The amplifiers are all tuned to a fixed frequency (called IF frequency) and an oscillator of variable tunable frequency is combined with the input signal in a nonlinear circuit to produce a new frequency (the difference of signal and oscillator frequency) equal to the IF frequency, which is then amplified. This will be discussed in Chapter 50.