We are now ready to investigate, more generally, what form the laws of mechanics take under the Lorentz transformation. [We have thus far explained how length and time change, but not how we get the modified formula for m (Eq. 15.1). We shall do this in the next chapter.] To see the consequences of Einstein’s modification of m for Newtonian mechanics, we start with the Newtonian law that force is the rate of change of momentum, or

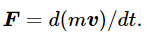
Momentum is still given by mv, but when we use the new m this becomes

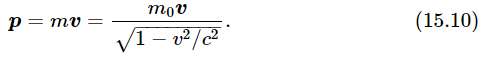
This is Einstein’s modification of Newton’s laws. Under this modification, if action and reaction are still equal (which they may not be in detail, but are in the long run), there will be conservation of momentum in the same way as before, but the quantity that is being conserved is not the old mv with its constant mass, but instead is the quantity shown in (15.10), which has the modified mass. When this change is made in the formula for momentum, conservation of momentum still works.

Now let us see how momentum varies with speed. In Newtonian mechanics it is proportional to the speed and, according to (15.10), over a considerable range of speed, but small compared with c, it is nearly the same in relativistic mechanics, because the square-root expression differs only slightly from 1. But when v is almost equal to c, the square-root expression approaches zero, and the momentum therefore goes toward infinity.

What happens if a constant force acts on a body for a long time? In Newtonian mechanics the body keeps picking up speed until it goes faster than light. But this is impossible in relativistic mechanics. In relativity, the body keeps picking up, not speed, but momentum, which can continually increase because the mass is increasing. After a while there is practically no acceleration in the sense of a change of velocity, but the momentum continues to increase. Of course, whenever a force produces very little change in the velocity of a body, we say that the body has a great deal of inertia, and that is exactly what our formula for relativistic mass says (see Eq. 15.10)—it says that the inertia is very great when v is nearly as great as c. As an example of this effect, to deflect the high-speed electrons in the synchrotron that is used here at Caltech, we need a magnetic field that is 2000 times stronger than would be expected on the basis of Newton’s laws. In other words, the mass of the electrons in the synchrotron is 2000 times as great as their normal mass, and is as great as that of a proton! That m should be 2000 times m₀ means that 1−v²/c² must be 1/4,000,000, and that means that v differs from c by one part in 8,000,000, so the electrons are getting pretty close to the speed of light. If the electrons and light were both to start from the synchrotron (estimated as 700 feet away) and rush out to Bridge Lab, which would arrive first? The light, of course, because light always travels faster.¹ How much earlier? That is too hard to tell—instead, we tell by what distance the light is ahead: it is about 1/1000 of an inch, or 1/4 the thickness of a piece of paper! When the electrons are going that fast their masses are enormous, but their speed cannot exceed the speed of light.

Now let us look at some further consequences of relativistic change of mass. Consider the motion of the molecules in a small tank of gas. When the gas is heated, the speed of the molecules is increased, and therefore the mass is also increased and the gas is heavier. An approximate formula to express the increase of mass, for the case when the velocity is small, can be found by expanding in a power series, using the binomial theorem. We get

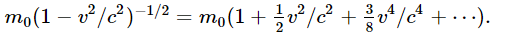
We see clearly from the formula that the series converges rapidly when v is small, and the terms after the first two or three are negligible. So, we can write

in which the second term on the right expresses the increase of mass due to molecular velocity. When the temperature increases the v² increases proportionately, so we can say that the increase in mass is proportional to the increase in temperature. But since 1/2 m₀v² is the kinetic energy in the old-fashioned Newtonian sense, we can also say that the increase in mass of all this body of gas is equal to the increase in kinetic energy divided by c², or Δm=Δ(K.E.)/c².