
أشباه البلورات والبلورات النانومترية
 المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
 المصدر:
علم البلورات والاشعة السينية
المصدر:
علم البلورات والاشعة السينية
 الجزء والصفحة:
ص413–415
الجزء والصفحة:
ص413–415
 2023-10-10
2023-10-10
 1658
1658
استقر في الأذهان ولفترات بعيدة أن المادة المكثفة تتجلى في صورة بلورة صلبة، بل إن فيزياء الجوامد ظلت هي فيزياء البلورات إلى حد بعيد. وقد مر بنا في الأبواب السابقة أن البلورات تتمتع بتماثل انتقالي كامل يؤدي بالضرورة إلى قواعد اختيار مهمة يمكن تطبيقها بنجاح عند تفسير نتائج التجارب ووضع النماذج النظرية المفسرة لسلوك الجوامد على أن الاهتمام بالمواد غير البلورية قد اتخذ أبعاداً كبيرة في العقود الأخيرة. وهنا يجب أن نفهم مصطلح «غير البلورية» على أنه افتقار المادة للتماثل الانتقالي الصريح، وتتراوح هذه المواد غير البلورية؛ من السوائل والمواد الصلبة الأمورفية إلى بعض البنى (جمع بنية) غير المتناسبة. إلا أن السوائل والمواد الأمورفية قد تحتوي على القليل من الانتظام الذي ينحصر أحيانا في تجمعات من الذرات. أما الهياكل غير المتناسبة فيمكن وصفها على أنها شبيكات دورية بها ذرات قد زحزحت مواضعها بالنسبة لمواقع الشبيكة. كما أن الشبيكة ودورية الإزاحات ليست في تناسب ثابت.
أما الهياكل شبه الدورية أو ما يطلق عليه «أشباه البلورات» «Quasi crystals» فهي مواد غير بلورية ولكنها تتمتع بنظام بعيد المدى، كما أنها تفتقر إلى دورية ثلاثية الأبعاد، بل وإلى شبيكة غير متناسبة الهيكل.
وقد درسنا أن عمليات التماثل الدورانية قد تتم عن طريق محاور ذات طيتين أو ثلاث أو أربع أو ست طيات، أما عمليات الدوران بواسطة محاور ذات خمس طيات أو أكثر من ست طيات فغير مسموح بها. ولو تخيلنا مجموعة من البلاطات الخماسية المستوية بحيث تكون زاوية كل رأس من الخمسة هي 108º لوجدنا أنها تحدث كل 3.333 مرة على مدى الزاوية 2π؛ ولذلك لا نستطيع توزيع سوى ثلاثة مضلعات وفجوة زاوية مقدراها 36º حول أية نقطة من «نقط الشبيكة» (شكل 14-1). وإذا افترضنا أيضا أن لدينا شبيكة برافيه ذات بعدين وأن الشبيكة مبنية على خلية خماسية الأضلاع فإن نقطة من نقط الشبيكة عند r1 وأخرى عند مركز الخلية سيحتمان أن تكون هناك نقطة عند r1–. وليس هذا ممكنا في واقع الأمر. (شكل 14-2). على أنه من الممكن استيفاء ذلك باختيار خلية أكبر ذات عشرة أضلاع (وهي الخلية المبينة منقطة في الشكل السابق). وفي هذه الحالة ستكون النقاط قد زحزحت من النقطة المركزية بمقدار المتجه r2 ولا تصبح منتمية إلى نقاط الشبيكة كما كان ينبغي لها أن تكون.

شكل (14-1)
بعض الخلايا الثلاثية والرباعية والسداسية التي تكون هيكلا دوريا. ويرى ايضا خلايا خماسية وسباعية
والخلايا ذات الأضلاع السبعة ليست هي الأخرى مسموحا بها حيث تبلغ زوايا الرؤوس '57 °128 وهي تتكرر 2.8 مرة في الزاوية π2، وإذا حاولنا رص هذه الخلايا جنبا إلى جنب لتكونت فجوات زاوية مقدار كل منها '86 °128 (الشكل 14-1).
أما في الحالة العامة، حيث متعدد الأضلاع (n ضلع) يحتوي على رؤوس زاوية كل منها 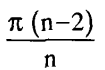 ، فنجد أن الترتيب الدوري ممكن الحدوث إذا كانت الزوايا تمثل كسرا حقيقيا من π2 أو كان المقدار
، فنجد أن الترتيب الدوري ممكن الحدوث إذا كانت الزوايا تمثل كسرا حقيقيا من π2 أو كان المقدار 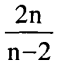 يساوي عددا صحيحا. وفيما عدا الأشكال الخماسية والسباعية فإن هذا العدد يصير على الترتيب 2.666، . . .، 2.2 بالنسبة المتعددات الأضلاع من الرتب الأكبر. ويظل هذا العدد اكبر من 2 على الدوام (فهو يصل إلى 2.0833 إذا كان عدد الأضلاع خمسين ضلعا).
يساوي عددا صحيحا. وفيما عدا الأشكال الخماسية والسباعية فإن هذا العدد يصير على الترتيب 2.666، . . .، 2.2 بالنسبة المتعددات الأضلاع من الرتب الأكبر. ويظل هذا العدد اكبر من 2 على الدوام (فهو يصل إلى 2.0833 إذا كان عدد الأضلاع خمسين ضلعا).
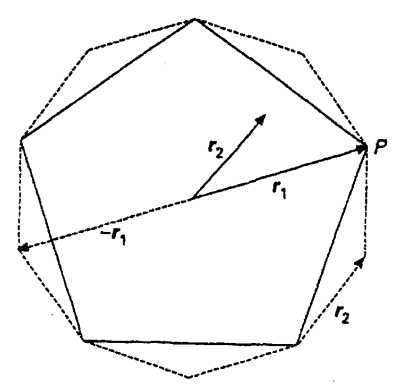
شكل (14-2)
لا تعتبر الخلايا الخماسية والعشارية متوافقة مع الدورية
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


