طريقة وارين لقياس العرض
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص337–338
2023-10-04
1442
يجب الأخذ في الاعتبار أنه حتى في حالة البلورات الكبيرة المثالية (perfect) تكون الانعكاسات ذات عرض محدد وهذا يرجع لعدة أسباب هي:
1- تفرق أو تباعد الأشعة الساقطة (divergence).
2- أبعاد العينة.
3- العرض الطبيعي لأشعة إكس نفسها.
وتوجد صعوبات نظرية للأخذ في الاعتبار هذه العوامل.
وفي سنة 1941 م اقترح وارين Warren أن مربع الأجزاء من عرض الخطوط يمكن جمعها على بعضها فإذا كان B هو العرض الكلي لخط الحيود، b هو العرض نتيجة الظروف العملية المذكورة سابقا فيكون β هو العرض نتيجة صغر حجم البلورات حيث يعطى بالمعادلة:
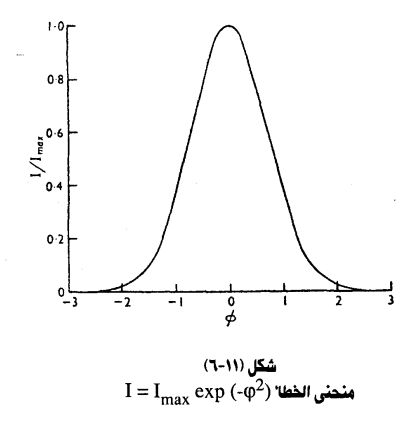
وإثبات هذه العلاقة يعتمد على فرضية أن توزيع الشدة على خط الانعكاس له الشكل:
ويسمى منحني الخطأ error curve حيث I هي شدة الأشعة المقاسة عند زاوية انحراف φ من القيمة الحقيقية للكميات θ، α هي كمية ثابتة وهذه الدالة الموضحة بشكل (11-6) اختيرت لأن لها القيمة العظمى عند = zero φ وتقل إلى الصفر كلما ازدادت قيمة φ، كما أنه في طريقة إثبات العلاقة السابقة يفترض أن عناصر الانعكاسات (elements of broadening) لها أيضا هذا الشكل.
ومن الواضح أن العرض الطبيعي للخط المنبعث لا يتوافق مع هذه الفرضية ذلك لأنه يحتوي على قمتين هما α1 ، α2 ويجب مراعاة أن يؤخذ في الاعتبار أن يكون BT هو العرض المشاهد عمليا بعد تصحيحه نتيجة وجود الثنائي 2α 1α.
وعمليا لا يمكن اعتبار طريقة وارين يمكن تطبيقها في جميع الأحوال لأن عناصر عرض الانعكاسات elements of broadening) لا يكون لها شكل منحني الخطأ.
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
اخر الاخبار
اخبار العتبة العباسية المقدسة
